General linear mixed effects model
Linear combinations of elements of beta
Determining estimability numerically
Substitution of estimable functions for non-estimable functions
Comparing the Linear Mixed Effects object to SAS PROC MIXED
References for Linear Mixed Effects
Phoenix’s Linear Mixed Effects object is based on the general linear mixed effects model, which can be represented in matrix notation as:
y = Xb + Zg + e
where:
X is the matrix of known constants and the design matrix for b.
b is the vector of unknown (fixed effect) parameters.
g is the random unobserved vector (the vector of random-effects parameters), normally distributed with mean zero and variance G.
Z is the matrix of known constants, the design matrix for g.
e is the random vector, normally distributed with mean zero and variance R.
g and e are uncorrelated. In the Linear Mixed Effects object, the Fixed Effects tab is used to specify the model terms for constructing X; the Random tabs in the Variance Structure tab specifies the model terms for constructing Z and the structure of G; and the Repeated tab specifies the structure of R.
In the linear mixed effects model, if R=s2I and Z=0, then the LinMix model reduces to the ANOVA model. Using the assumptions for the linear mixed effects model, one can show that the variance of y is: V = ZGZT + R.
If Z does not equal zero, i.e., the model includes one or more random effects, the G matrix is determined by the variance structures specified for the random models. If the model includes a repeated specification, then the R matrix is determined by the variance structure specified for the repeated model. If the model does not include a repeated specification, then R is the residual variance, that is R = s2I.
It is instructive to see how a specific example fits into this framework. The fixed effects model is shown in the “Linear mixed effects scenario” section. Listing all the parameters in a vector, one obtains: bT – [m,p1,p2,d1,d2,t1,t2]
For each element of b, there is a corresponding column in the X matrix. In this mode, the X matrix is composed entirely of ones and zeros. The exact method of constructing it is discussed under “Construction of the X matrix”, below.
For each subject, there is one Sk(j). The collection can be directly entered into g. The Z matrix will consist of ones and zeros. Element (i, j) will be one when observation i is from subject j, and zero otherwise. The variance of g is of the form
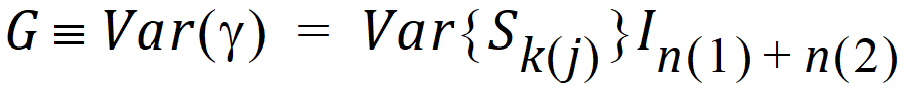
where Ib represents a b´b identity matrix.
The parameter to be estimated for G is Var{Sk(j)}. The residual variance is:
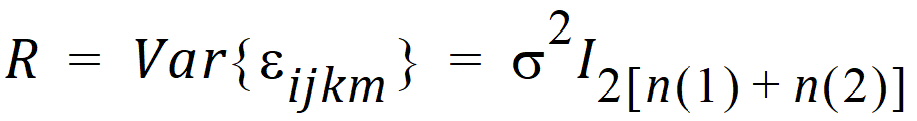
The parameter to be estimated for R is s2.
A summary of the option tabs and the part of the model they generate follows.
Fixed Effects tab specifies the X matrix and generates b.
Variance Structure tab specifies the Z matrix.
The Random sub-tab(s) generates G = var(g).
The Repeated tab generates R=var(e).
Additional information is available on the following topics regarding the linear mixed effects general model: