Determining estimability numerically
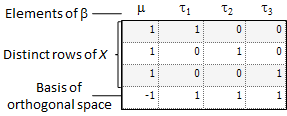
The X matrix for the model has three distinct rows, and these are shown in the table below. Also shown in the same table is a vector (call it z) that is a basis of the space orthogonal to the rows of X. Let l be a vector whose elements are the lj of the linear combination expression. The linear combination in vector notation is lTb and is estimable if lTZ=0. Allow for some rounding error in the computation of z. The linear combination is estimable if:
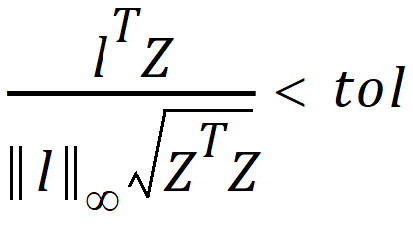
where || l ||¥ is the largest absolute value of the vector, and tol is the Estimability Tolerance.
In general, the number of rows in the basis of the space orthogonal to the rows of X is equal the number of linear dependencies among the columns of X. If there is more than one z, then previous equation must be satisfied for each z. The following table shows the basis of the space orthogonal to the rows of X.