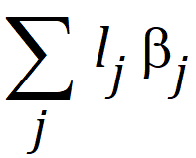Linear combinations of elements of beta
Most of the inference done by LinMix is done with respect to linear combinations of elements of b. Consider, as an example, the model where the expected value of the response of the jth subject on the ith treatment is:
m + ti
where m is a common parameter and m + ti is the expected value of the ith treatment.
Suppose there are three treatments. The X matrix has a column of ones in the first position followed by three treatment indicators.
The b vector is: b = [b0 b1 b2 b3] = [m t1 t2 t3]
The first form is for the general representation of a model. The second form is specific to the model equation shown at the beginning of this section. The expression:
with the lj constant, is called a linear combination of the elements of b.
The range of the subscript j starts with zero if the intercept is in the model and starts with one otherwise. Most common functions of the parameters, such as m+t1, t1 – t3, and t2, can be generated by choosing appropriate values of lj. Linear combinations of b are entered in LinMix through the Estimates and Contrasts tabs. A linear combination of b is said to be estimable if it can be expressed as a linear combination of expected responses. In the context of the model equation (shown at the beginning of this section), a linear combination of the elements of b is estimable if it can be generated by choosing c1, c2, and c3.
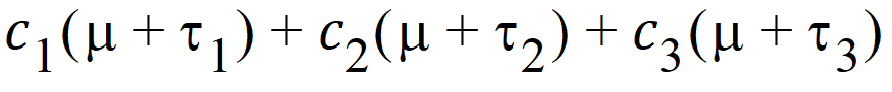
Note that c1=1, c2=0, and c3=0 generates m+t1, so m+t1 is estimable. A rearrangement of the expression is:
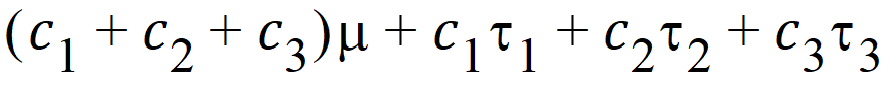
This form of the expression makes some things more obvious. For example, lj=cj for j=1,2,3. Also, any linear combination involving only ts is estimable if, and only if, l1+l2+l3=0. A linear combination of effects, where the sum of the coefficients is zero, is called a contrast. The linear combination t1 – t3 is a contrast of the t’s and thus is estimable. The linear combination t2 is not a contrast of the t’s and thus is not estimable.