A term is a variable or a product of variables. A model is specified by giving a sum of terms. For example, if A and B are variables in the dataset: A + B + AB.
Linear Mixed Effects takes this sum of terms and constructs the X matrix. The way this is done depends upon the nature of the variables A and B.
By default, the first column of X contains all ones. The LinMix object references this column as the intercept. To exclude it, select the No Intercept checkbox in the Fixed Effects tab. The rules for translating terms to columns of the X matrix depend on the variable types, regressor/covariate or classification. This is demonstrated using two classification variables, Drug and Form, and two continuous variables, Age and Weight, in Table 1. A term containing one continuous variable produces a single column in the X matrix.
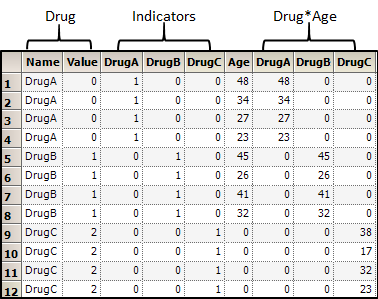
An integer value is associated with every level of a classification variable. The association between levels and codes is determined by the numerical order for converted numerical variables and by the character collating sequence for converted character variables. When a single classification variable is specified for a model, an indicator variable is placed in the X matrix for each level of the variable. Table 1 demonstrates this for the variable Drug.
The model specification allows products of variables. The product of two continuous variables is the ordinary product within rows. The product of a classification variable with a continuous variable is obtained by multiplying the continuous value by each column of the indicator variables in each row. For example, Table 1 shows the product of Drug and Age. Refer to Table 2 and Table 3.
The product operations described in the preceding paragraph can be succinctly defined using the Kronecker product. Let A=(aij) be a m´n matrix and let B=(bij) be a p´q matrix. Then the Kronecker product A Ä B=(aij B) is an mp ´ nq matrix expressible as a partitioned matrix with aij B as the (i, j)th partition, i=1,…, m and j=1,…,n.
For example, consider the fifth row of Table 1. The product of Drug and Age is:
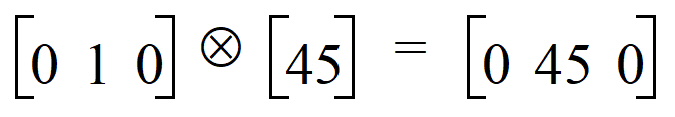
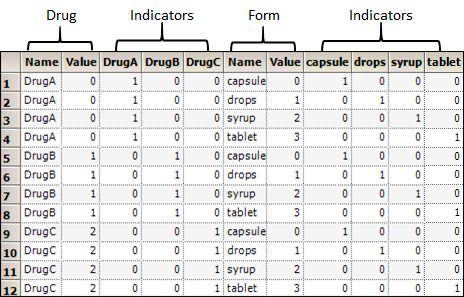
Now consider the fifth row of Table 2. The product of Drug and Form is:
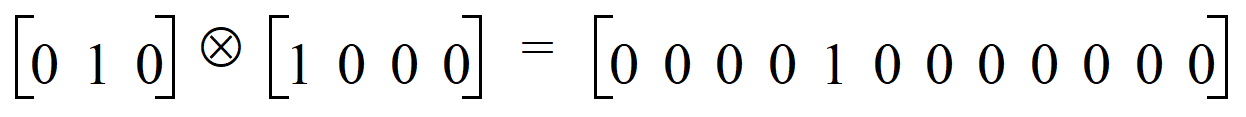
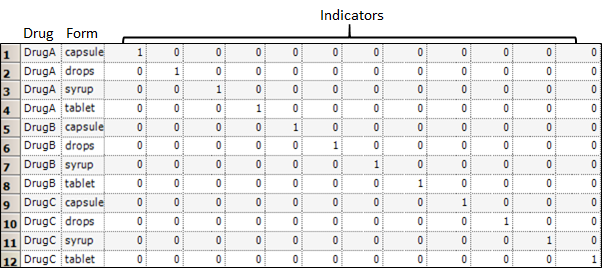
The result is the fifth row of Table 3.
Table 1: Indicator Variables and Product of Classification with Continuous Variables
Table 2: Classification Plus Indicator Variables