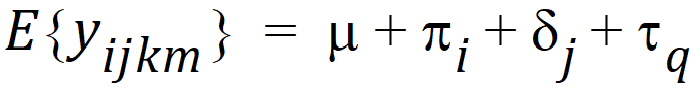The following example is used as a framework for discussing the functions and computations of the Linear Mixed Effects object.
An investigator wants to estimate the difference between two treatments for blood pressure, labeled A and B. Because responses are fairly heterogeneous among people, the investigator decided that each study subject will be his own control, which should increase the power of the study. Therefore, each subject will be exposed to treatments A and B. Since the treatment order might affect the outcome, half the subjects will receive A first, and the other half will receive B first. For the analysis, note that this crossover study has two periods, 1 and 2, and two sequence groups AB and BA.
The model will be of the form:
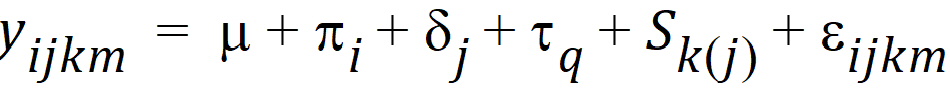
where:
i is the period index (1 or 2)
j is the sequence index (AB or BA)
k is the subject within sequence group index (1…nj)
m is the observation within subject index (1, 2)
q is the treatment index (1, 2)
m is the intercept
pi is the effect due to period
dj is the effect due to sequence grouping
tq is the effect due to treatment, the purpose of the study
Sk(j) is the effect due to subject
eijkm is the random variation
Typically, eijkm is assumed to be normally distributed with mean zero and variance s2 > 0. The purpose of the study is to estimate t1 – t2 in all people with similar inclusion criteria as the study subjects. Study subjects are assumed to be randomly selected from the population at large. Therefore, it is desirable to treat subject as a random effect. Hence, assume that subject effect is normally distributed with mean zero and variance Var(Sk(j)) ³ 0.
This mixing of the regression model and the random effects is known as a mixed effect model. The mixed effect model allows one to model the mean of the response as well as its variance. Note that in the model equation above, the mean is:
and the variance is given by:
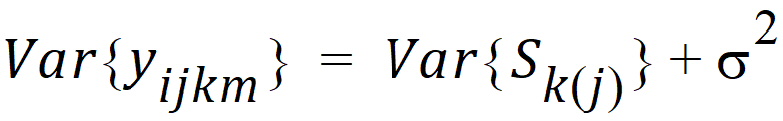
E{yijkm} is known as the fixed effects of the model, while Sk(j)+eijkm constitutes the random effects, since these terms represent random variables whose variances are to be estimated. A model with only the residual variance is known as a fixed effect model. A model without the fixed effects is known as a random effect model. A model with both is a mixed effect model.
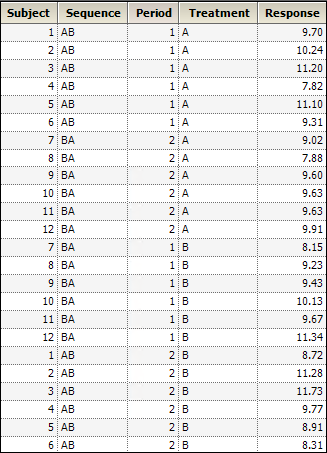
The data are shown in the table below. The Linear Mixed Effects object is used to analyze these data. The fixed and random effects of the model are entered on different tabs of the Diagram view. This is appropriate since the fixed effects model the mean of the response, while the random effects model the variance of the response.
The Linear Mixed Effects object can fit linear models to Gaussian data. The mean and variance structures can be simple or complex. Independent variables can be continuous or discrete, and no distributional assumption is made about them.
This model provides a context for the linear mixed effects model.