The LinMix Variance Structure tab specifies the Z, G, and R matrices defined in the “General linear mixed effects model” introduction. There may be zero, one, or more random effects but only one repeated effect may be specified. The Repeated effect specifies the R=Var(e). The Random effects specify Z and the corresponding elements of G=Var(g).
Multiple random effects vs. multiple effects on one random effect
Covariance structure types in the Linear Mixed Effects object
The repeated effect is used to model a correlation structure on the residuals. Specifying the repeated effect is optional. If no repeated effect is specified, then R=s2 IN is used, where N denotes the number of observations, and IN is the N ´ N identity matrix.
All variables used on this tab of the Linear Mixed Effects object must be classification variables.
To specify a particular repeated effect, one must have a classification model term that uniquely identifies each individual observation. Put the model term in the Repeated Specification field. Note that a model term can be a variable name, an interaction term (e.g., Time*Subject), or a nested term (e.g., Time(Subject)).
The variance blocking model term creates a block diagonal R matrix. Suppose the variance blocking model term has b levels, and further suppose that the data are sorted according to the variance blocking variable. Then R would have the form:
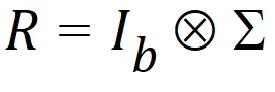
where S is the variance structure specified.
The variance S is specified using the Type pull-down menu. Several variance structures are possible, including unstructured, autoregressive, heterogeneous compound symmetry, and no-diagonal factor analytic. See the Help file for the details of the variance structures. The autoregressive is a first-order autoregressive model.
To model heterogeneity of variances, use the group variable. Group will accept any model term. The effect is to create additional parameters of the same variance structure. If a group variable has levels g=1, 2,…, ng, then the variance for observations within group g will be Sg.
An example will make this easier to understand. Suppose five subjects are randomly assigned to each of three treatment groups; call the treatment groups T1, T2, and T3. Suppose further that each subject is measured in periods t=0, 1, 2, 3, and that serial correlations among the measurements are likely. Suppose further that this correlation is affected by the treatment itself, so the correlation structure will differ among T1, T2, and T3. Without loss of generality, one may assume that the data are sorted by treatment group, then subject within treatment group.
First consider the effect of the group. It produces a variance structure that looks like:
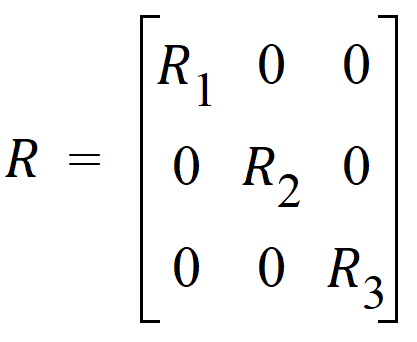
where each element of R is a 15´15 block. Each Rg has the same form. Because the variance blocking variable is specified, the form of each Rg is:
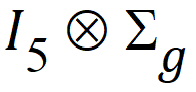
I5 is used because there are five subjects within each treatment group. Within each subject, the variance structured specified is:
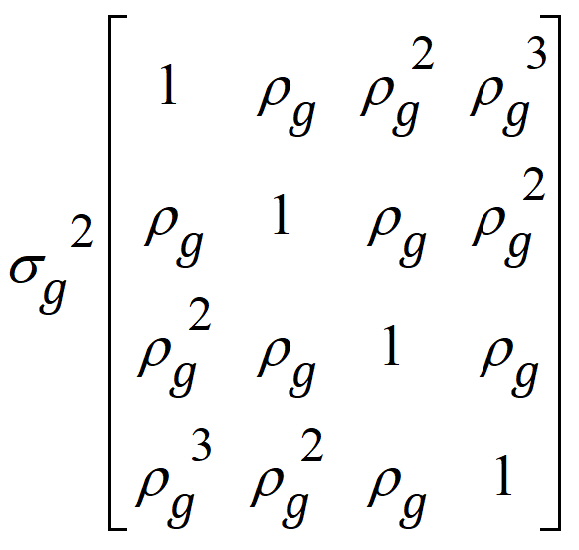
This structure is the autoregressive variance type. Other variance types are also possible. Often compound symmetry will effectively mimic autoregressive in cases where autoregressive models fail to converge.
The output will consist of six parameters: s2 and r for each of the three treatment groups.
Unlike the (single) repeated effect, it is possible to specify up to 10 random effects. Additional random effects can be added by clicking Add Random. To delete a previously specified random effect, click Delete Random. It is not possible to delete all random effects; however, if no entries are made in the random effect, then it will be ignored.
Model terms entered into the Random Effects model produce columns in the Z matrix, constructed in the same way that columns are produced in the X matrix. It is possible to put more than one model term in the Random Effects Model but each random page will correspond to a single variance type. The variance matrix appropriate for that type is sized according to the number of columns produced in that random effect.
The Random Intercept checkbox puts an intercept column (that is, all ones) into the Z matrix.
The Variance Blocking Variables has the effect of inducing independence among the levels of the Variance Blocking Variables. Mathematically, it expands the Z matrix by taking the Kronecker product of the Variance Blocking Variables with the columns produced by the intercept checkbox and the Random Effects Model terms.
The Group model term is used to model heterogeneity of the variances among the levels of the Group model term, similarly to Repeated Effects.
Multiple random effects vs. multiple effects on one random effect
Suppose one has two random effect variables, R1 and R2. Suppose further that R1 has three levels, A, B, and C, while R2 has two levels, Y and Z. The hypothetical data are shown as follows.
R1 values: A, B, C, A, B, C
R2 values: Y, Y, Y, Z, Z, Z
Specifying a random effect of R1+R2 will produce different results than specifying R1 on Random 1 and R2 on Random 2 pages. This example models the variance using the compound symmetry variance type. To illustrate this, build the resulting Z and G matrices.
For R1+R2 on Random 1 page, put the columns of each variable in the Z matrix to get the following.
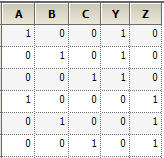
The random effects can be placed in a vector: g = (g1,g2,g3,g4,g5)
R1 and R2 share the same variance matrix G where:
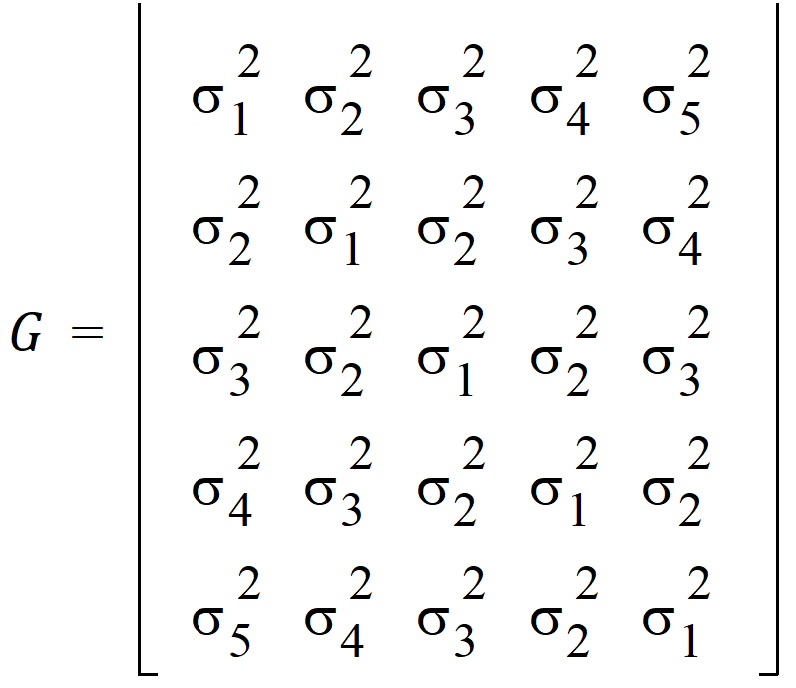
Now, consider the case where R1 is placed on Random 1 tab, and R2 is placed on Random 2 tab. For R1, the Z matrix columns are:
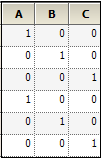
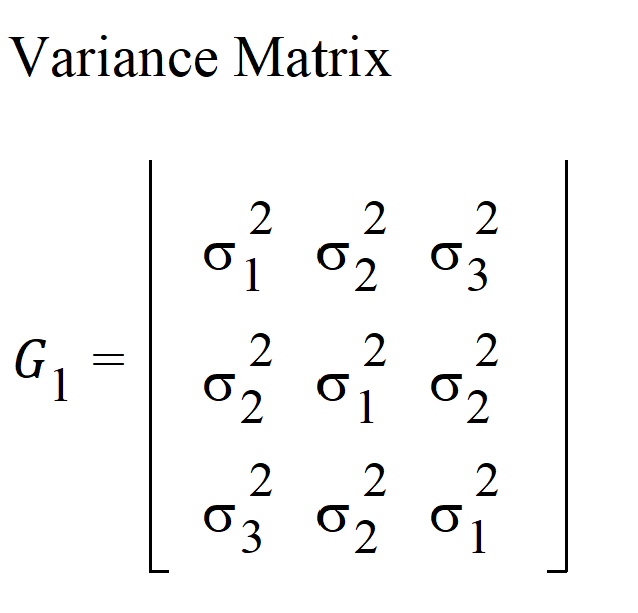
For R2, the columns in the Z matrix and the corresponding G is:
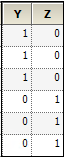
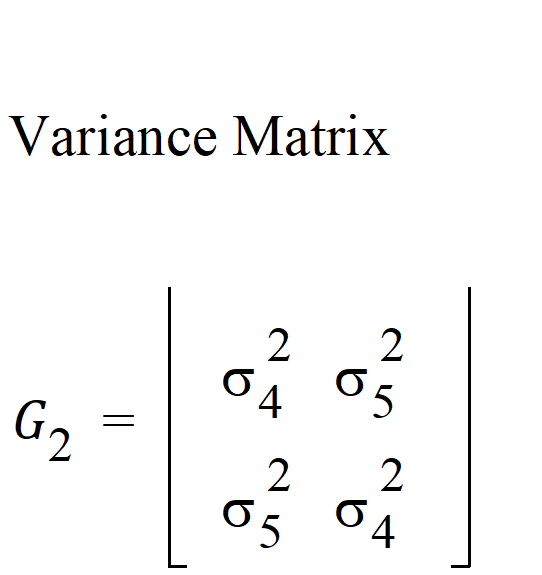
In this case:
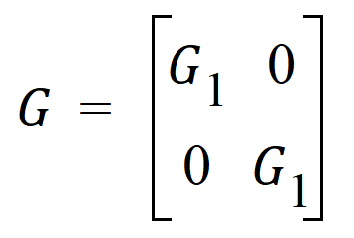
Covariance structure types in the Linear Mixed Effects object
The Type menu in the Variance Structure tab allows selecting a variety of covariance structures. The variances of the random-effects parameters become the covariance parameters for this model. Mixed linear models contain both fixed effects and random effects parameters. For more on variance structures see the “Variance structure” section for an explanation of variance in linear mixed effects models. See the “Covariance structure types” section in the Bioequivalence documentation for descriptions of covariance structures.