Explore the Formulation of FOCE
Consider the case where the linearization method is used to approximate the Hessian of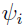 
, and both 
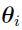and 
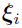are chosen to be the conditional mode 
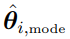obtained with population parameter 
, 
, 
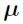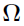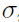and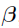 
, i = 1, 2,..., NSUB. For this case, using the equation (discussed earlier)
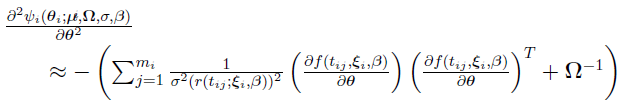
the Hessian of 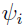is approximated by
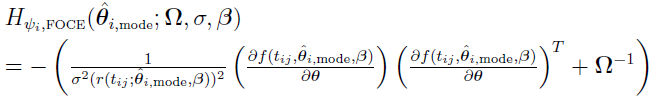
which is often called the FOCE Hessian approximation.
Since the approximate marginal PDF for this case depends on the conditional modes, it is implemented in two different ways:
FOCE-LB Formulation: iteratively minimize to obtain individual estimates with respect to current population parameter estimates, then maximize resulting approximate marginal PDF to attain a new set of population parameter estimates
FOCE-ELS Formulation: conceptually involves only a single top-level optimization of the approximate marginal PDF
This approach iteratively minimizes the equation
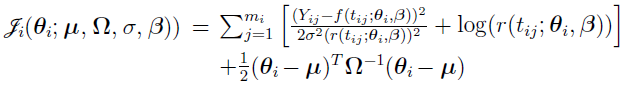
(discussed earlier) to obtain individual estimates with respect to current population parameter estimates (referred to as the conditional step) and then maximizes the resulting approximate marginal PDF to obtain a new set of population parameter estimates.
At the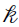 
th iteration, 
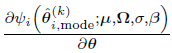is usually not equal to zero unless 
, 
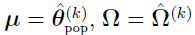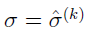, and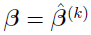 
. Thus, by the equation:
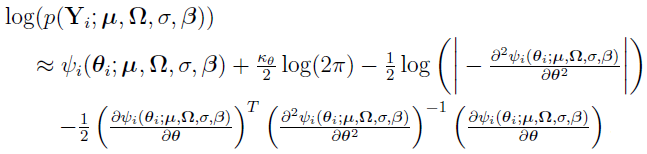
(discussed earlier), for the Laplacian approximation based FOCE-LB, the approximate marginal PDF also involves calculation of the gradient of 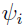. This is also approximated by the linearization method as given by
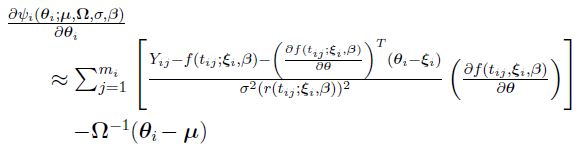
which indicates that, for this case, 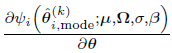is approximated by
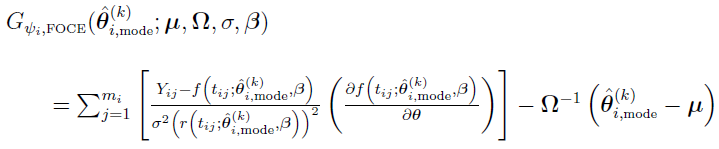
Thus, by this and the following equations
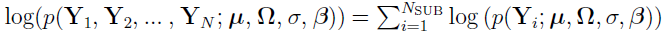
(discussed in “Laplacian-Approximation-Based Algorithms”)
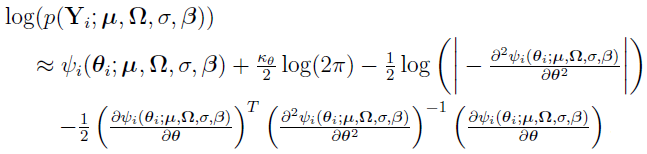
(discussed in “Laplacian Approximation Method and the Resulting Algorithms”)
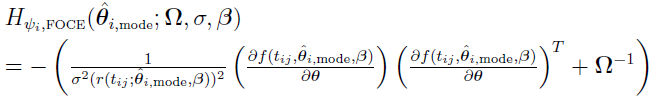
(discussed in “Explore the Formulation of FOCE”)
the negative of the approximate marginal PDF for the Laplacian approximation based FOCE-LB is given by
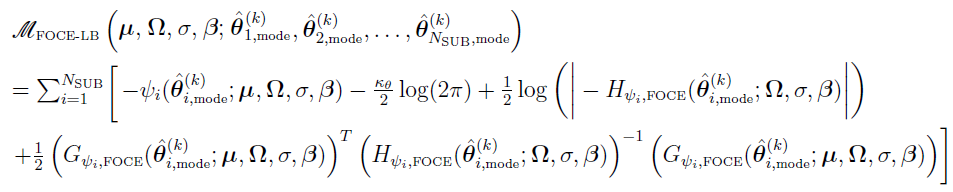
FOCE-ELS Formulation
The FOCE-ELS approach conceptually involves only a single top-level optimization of the approximate marginal PDF, where each evaluation of the approximate marginal PDF requires a conditional step, as in the FOCE-LB approach. Using the following equations (discussed in “Laplacian Approximation Method and the Resulting Algorithms”)
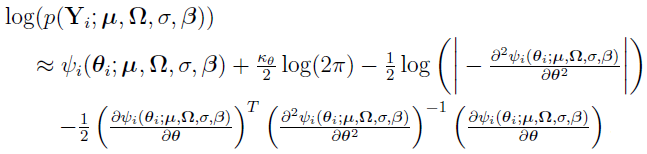
and
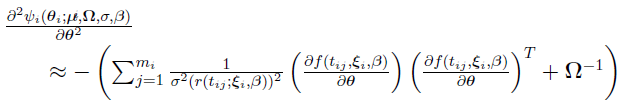
the top-level objective function is given by
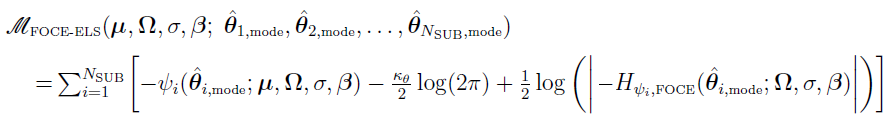
where
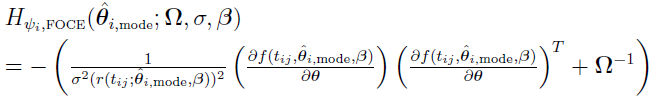
as discussed in “Linearization Method and the Resulting Algorithms”).