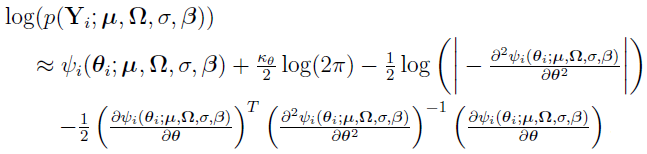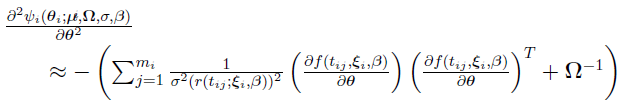Laplacian Approximation Method and the Resulting Algorithms
Now consider using the Laplacian approximation method to approximate the marginal PDF.
Let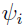 
be the logarithm of the joint PDF of 
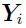and 
:
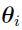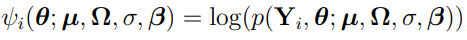
Then, using the earlier equation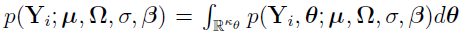 
, the marginal PDF can be expressed as 
.
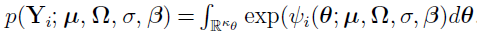The Laplacian approximation method involves approximating 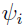by its second-order Taylor expansion around a point 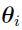, where 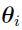is chosen such that 
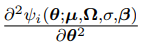is negative definite. With this approximation, the logarithmic equation becomes:
Thus, the Laplacian approximation method involves calculating the second-order derivatives of the logarithm of joint PDF with respect to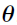 
. In addition, if 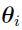is not chosen as the mode of 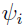, then it also involves calculation of the first-order derivatives.
Sometimes it is difficult to calculate the Hessian of 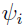. In such cases, the linear approximation equation, discussed earlier:
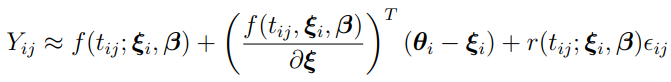
is often used to get an approximation of it. From this linear approximation, the conditional PDF of , given , becomes:
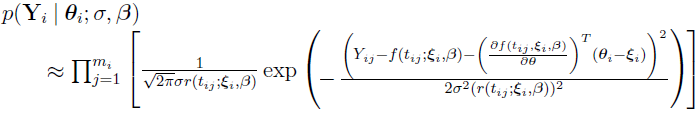
Hence, using the above equation and the following equation (discussed earlier)
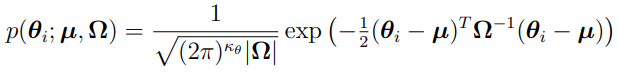
the logarithm of the joint PDF of 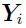and 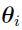is approximated by
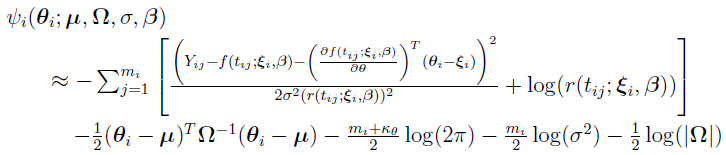
The gradient and the Hessian of 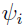, respectively, are then approximated by
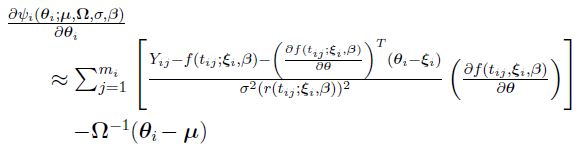
Note that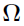 
is positive definite. Hence, by the above equation, the Hessian matrix obtained by the linearization method is a constant matrix and is negative definite.