Laplacian-Approximation-Based Algorithms
The following statements briefly introduce the Laplacian-Approximation-based algorithms. Click a link for additional details. For a more mathematical look at the Laplacian-Approximation method refer to “Review of Laplacian-Approximation Formulation”.
The FO method does not involve inner optimization problem and hence it is computationally much faster than the FOCE methods. However, it is far less accurate than the FOCE methods due to the poor approximation.
Since FOCE-ELS involves NSUB inner-level optimization for each evaluation of top-level objective function, it is usually considerably slower than the FOCE-LB, but its progress is monotonic from iteration to iteration while this may not be true for FOCE-LB.
Since the linear approximation involved in the Laplacian approximation based FO, FOCE-LB and FOCE-ELS methods depend on the assumption that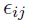 
s are i.i.d. normally distributed. Hence, these methods are only applicable to normal/Gaussian data.
The Laplacian method involves calculating Hessian of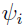 
. Hence, it is often regarded as slightly more accurate but slower and numerically less reliable than the FOCE method. However, since the approximation does not depend on the normal assumption for 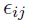s, the Laplacian engine is applicable for both Gaussian and non-Gaussian data (e.g., count, categorical, and time-to-event data).