The FOCE (First Order Conditional Estimation) Laplacian-approximation-based method was developed around the 1990s [7] and applies only to observational data that are continuous and modeled with a Gaussian likelihood. As with FO, the random effects (
) are assumed normally distributed as are the residuals (
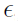). This implies that a first-order linearization of the model with respect to and 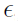will have a normal (Gaussian) distribution of values when evaluated at a given time point for a random individual.
In Phoenix NLME, there are two FOCE implementations:
FOCE Lindstrom-Bates (FOCE L-B)
FOCE Extended Least-Squares (FOCE ELS)
The two implementations are based on different inner optimization procedures. However, both use “interaction,” which means that the individual prediction, obtained by using the current optimal estimates to compute the model prediction function, is used to evaluate the residual error model. In contrast, the FO algorithm uses the population prediction, obtained by setting = 0, to evaluate the residual error model. The interaction computation is usually regarded as leading to more accurate overall estimates of THETA, SIGMA, and OMEGA.
For a more mathematical look at the FOCE algorithm, refer to “Explore the Formulation of FOCE”.