FOCE L-B solves a sequence of linearized mixed effects problems. Each iteration consists of the following steps:
Conditional step: for each individual, the application finds the optimal 
values corresponding to the current (
, 
, 
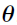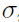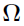) estimates by maximizing the joint log likelihood with respect to . This optimization is performed with a quasi-Newton optimization algorithm also used in step 3 as well as other model engines.
Linearize the model function with respect to the s around the optimal values computed in step 1. The linearization is used to compute an FOCE approximation of the marginal log likelihood function.
Solve the linearized mixed effects problem by minimizing the FOCE approximation to the overall negative marginal log likelihood of the linearized problem to obtain a new set of estimates (, , ).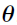
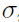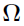The iterations are repeated until convergence, which is defined by reduction of the gap or the difference between starting and final optimal log likelihood values for the current linearized problem, to less than a specified tolerance (by default 0.001). Note that convergence need not be monotonic. That is, the gaps do not always decrease, and the log likelihoods of the solutions to the linearized problems do not necessarily improve from iteration to iteration.
FOCE L-B usually converges, but there is no theoretical guarantee of convergence and both oscillatory and divergent behavior might occasionally occur. The final converged parameter values represent the optimal FOCE solution to the final linearized problem, and are usually, but not necessarily, close to the optimal FOCE ELS solution.