Discrete and distributed delays
References – Distributed Delays
Transit compartment models, described by systems of ordinary differential equations (ODEs), have been widely used to describe delayed outcomes in pharmacokinetics and pharmacodynamics studies. The obvious disadvantage for this type of model is it requires manually finding proper values for the number of compartments, and hence it is time-consuming. It is also difficult, if not impossible, to do population analysis using this model. In addition, it may require many differential equations to fit the data and may not adequately describe some complex features.
To alleviate these advantages, a distributed delay approach was proposed in “Hu, Dunlavey, Guzy, and Teuscher (2018)” to model delayed outcomes in pharmacokinetics and pharmacodynamics studies. It involves convolution of the signal to be delayed (S) and the probability density function (g) of the delay time,
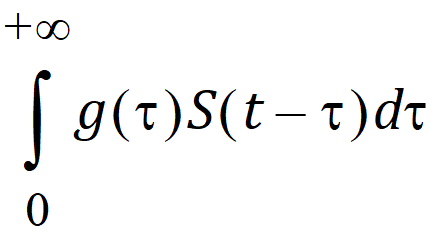
Thus, for the distributed delay approach, the delay time may vary among signal mediators (e.g., drug molecules or cells), and hence it is a natural extension of the discrete delay approach that S(t – t) in which case, where the delay time is assumed to be the same (i.e., t) for all signal mediators.
Differential equations involving discrete delays and/or distributed delays are called delay differential equations (DDEs). The difference between ODEs and DDEs is that the future state of the system governed by ODEs is totally determined by its present value while for DDEs it is determined not only by its present value but also by its past. This means that, for DDEs, one must specify the values of the system state prior to the system starts (assuming throughout that the system starts at time zero). For example, for the following differential equation with a distributed delay,
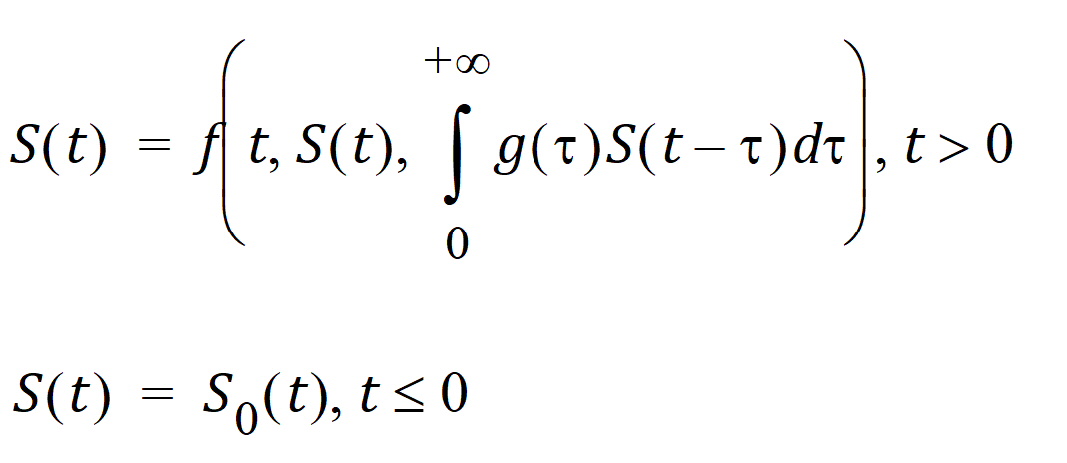
one must specify the values of S(t) over all negative t; that is, one must specify S0, which is often called the history function.
It was shown in “Hu, Dunlavey, Guzy, and Teuscher (2018)” that the distributed delay approach is general enough to incorporate a wide array of pharmacokinetic and pharmacodynamic models as special cases, including transit compartment models, effect compartment models, indirect response models with production either simulated or inhibited, typical absorption models (either zero-order or first-order absorption), and several atypical (or irregular) absorption models (e.g., parallel first-order, mixed first-order, and zero-order, inverse Gaussian, and Weibull absorption models). This was done through assuming a specific distribution form for the delay time.
Specifically, transit compartment models assume that the delay time is Erlang distributed, with shape and rate parameters respectively determining the number of transit compartments and the transition rate between the compartments. Note that Erlang distribution is a special case of the gamma distribution, which allows for non-integer shape parameters. Hence, distributed delay models with delay time assumed to be gamma distributed (referred to as gamma distributed delay models) are natural extension of transit compartment models. Examples for extending transit compartment models to their corresponding gamma distributed delay models can be found in “Hu, Dunlavey, Guzy, and Teuscher (2018)” and “Krzyzanski, Hu, and Dunlavey (2018)”.