PML provides an alternative function, gammaDelay, to describe a gamma distributed delay. The difference between the gammaDelay function and the delay function with dist = Gamma is how the integral is approximated. The delay function involves direct numerical calculation of the integral with the values of the signal to be delayed recorded in a table upon every derivative evaluation and, hence, it may become expensive or even prohibitive for complex population analysis. The gammaDelay function, on the other hand, is based on the ODE approximation method provided in Krzyzanski, 2019, wherein it was shown that this approach is much faster than the delay function.
The syntax of the gammaDelay function is given as follows:
gammaDelay(S, MeanDelayTime
, shape = ShapeParam
[, hist = HistExpression]
, numODE = NumberOfODEUsed
)
Here S denotes the signal to be delayed. The second argument denotes the mean for the gamma distribution. The shape option must be provided and it is used to specify the shape parameter of the gamma distribution. The hist option is used to specify the value of S prior to time 0. If this option is not provided, then it is automatically assumed that S(t)=0 for t<0. The numODE option must be provided and it is used to specify the number of ODEs used to approximate the integral. The maximum number of ODEs allowed is 400.
The accuracy of the approximation for the gammaDelay function depends on the number of ODEs used: the higher the number of ODEs used, the more accurate the approximation. However, the performance cost increases as the number of ODEs increases. In addition, many ODEs may lead to numerical difficulties in the ODE solver. Hence, some exploratory analysis of the effect of number of ODEs on the solution of the given problem is recommended. Here is a general guideline, given in Krzyzanski, 2019, on the number of ODEs used: if the shape parameter for the gamma distribution is greater than one, then at least 21 ODEs are needed; otherwise, more than 101 ODEs are needed.
The gammaDelay function can also be put on the right-hand side of a differential equation. In addition, the mean and shape parameter for the gamma distribution can be estimated. The example project OneCpt0OrderAbsorp_gammaDelayEmax.phxproj (located in …\Examples\NLME) demonstrates how to use the gammaDelay function to describe a delayed drug response given below:
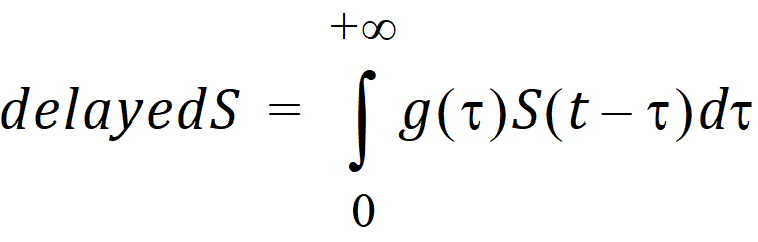
Here g is the probability density function of a gamma distribution with mean being MeanDelayTime and shape parameter being ShapeParam, and S is described by an Emax model:
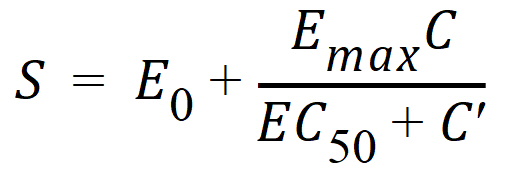
where the drug concentration, C, is described by a one-compartment model with zero-order absorption and first-order elimination. Note that C(t) = 0 for t £ 0. Hence S(t) = E0 for t £ 0. Thus, the PML code for the delayed drug response is given as follows:
delayedS = gammaDelay(S, MeanDelayTime
, shape = ShapeParam
, hist = E0
, numODE = 21
)
where the value of numODE is chosen based on some exploratory analysis (see the workflow Effect_NumODE_Solution in the project, which shows that the solutions obtained using 21 ODEs are similar to ones obtained using 41 or 81 ODEs). The model fitting results (given in the workflow Estimation) show that the shape parameter and the mean delay time can be reliably estimated along with the other parameters, and that standard diagnostic plots are good.