Differential equations in NLME
Prediction and Prediction Variance Corrections
Shrinkage calculation
Differential equations in NLME
Ordinary differential equations can be solved for Phoenix models by several methods. These methods available under the option Max ODE in the Run Options tab.
Matrix Exponent option
Stiff option — LSODE
Auto-Detect option — LSODA
Non-Stiff option — DVERK
Non-Stiff option — DOPRI5
The ODE solvers used by Phoenix have three accuracy controls that are available in the Advanced Run Options tab:
ODE Rel. Tol.: Relative tolerance (RTOL)
ODE Abs. Tol.: Absolute tolerance (ATOL)
ODE max step: Maximum number of allowable steps or function evaluations (depending on the solver) to achieve the above accuracies (MAXSTEP)
For more information, see “RTOL, ATOL, and MAXSTEP ODE error controls”.
This is the default option for solving ordinary differential equations for Phoenix models. It requires that the system be expressible as dy/dt=Jy, where J is a matrix (the Jacobian) with elements that are constant over a time interval.
The general N-compartment model governed by ordinary differential equations takes the form:
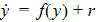
where y =(y1, …, yN)T is an N-dimensional column vector of amounts in each compartment as a function of time, f(y) is a column vector-valued function that gives the structural dependence of the time derivatives of y on the compartment amounts, and r is an N-dimensional column vector of infusion rates into the compartments. Note that as opposed to the closed-form solution of first-order models, dosing can be made into any combination of compartments, and all of the compartments are modeled.
To account for infusion rates, define the augmented system:
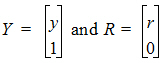
In the special first-order case, the equations are represented as:
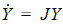
where J is the Jacobian matrix given by:
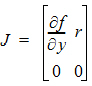
The partial derivatives are obtained by symbolic differentiation of f(y). If any of them are not constant (over the given time interval), matrix exponent cannot be used. In such cases, Phoenix automatically switches the ODE solver from the matrix exponent to the DVERK except in the case where the model involves gammaDelay function (for this case, it automatically switches to DOPRI5). It is worth pointing out that the actual ODE solver requested/used can be found at the beginning of the Core Output tab (Text Output Results section).
Assuming J is constant, the state vector Y evolves according to:
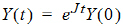
where eJt is defined by the Taylor series expansion of the standard exponential function. Standard math library routines are available for the computation of the matrix exponential. These are faster and more accurate than the equivalent computation with a numerical ODE solver and do not suffer from stiffness.
In the steady state case where a vector bolus dose is given at intervals of length, the solution takes the form:
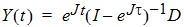
where D is a column vector giving the amount of the bolus deposited in each compartment.
In the case where the matrix exponent cannot be used, the steady state is found by pre-running the model via the ODE solver for enough multiples of t so that Y changes by less than a tolerance.
LSODE (Livermore Solver for Ordinary Differential Equations) is the ODE solver used by Phoenix to solve stiff systems of the form dy/dt=f. It treats the Jacobian matrix df/dy as either a dense (full) or a banded matrix, and as either supplied automatically by Phoenix or internally approximated by difference quotients (if Phoenix fails to generate it).
Stiff systems typically arise from models with processes that proceed at very different rates, for example, very slow equilibration of a peripheral compartment with a central compartment relative to the rate at which elimination occurs from the central compartment. Generally, a stiff solver outperforms, in terms of both time and accuracy, a non-stiff solver for such systems, but the non-stiff solver can be superior for non-stiff systems.
Nonlinear systems can change from stiff to non-stiff during evaluation, which can result in incorrect estimates and/or much longer execution times if the incorrect ODE solver is selected. LSODA (written by Linda R. Petzold and Alan C. Hindmarsh) is a variant version of the LSODE solver and it automatically selects between non-stiff (Adams) and stiff (Backward Differentiation Formula) methods. LSODA is a very robust adaptive stepwise solver that uses the non-stiff method initially, and dynamically monitors data in order to decide which method to use.
This is an explicit Runge-Kutta method based on Verner’s fifth and sixth order pair of formula. Due to its fast and robust performance, it is one of the widely used methods for solving non-stiff problems and is also the default solver used by Phoenix when the matrix exponent solver is not applicable.
It is well-known that the explicit Runge-Kutta methods cannot compete with specifically designed stiff methods, except for very mildly stiff systems. For the stiff problems, integration errors are expected. The user is advised to switch to the LSODE/LSODA solver.
DOPRI5 is another widely used solver for the non-stiff problems. It is an explicit Runge-Kutta method of order (4)5, based on Dormand-Prince pair. More specifically, it uses six function evaluations to calculate fourth- and fifth-order accurate solutions. Numerical experiments show that DOPRI5 may be more reliable and efficient than the DVERK, in certain stiff problems.
RTOL, ATOL, and MAXSTEP ODE error controls
The default values for ATOL and RTOL are 0.000001, while the default value of MAXSTEP is 50000.
-
Matrix Exponent solver
For the matrix exponent solver, only an absolute tolerance (ATOL) applies. If ATOL is set to zero, it is reset internally to the square root of the machine precision (approximately 1.e-8). For a full discussion, see Sidje, Roger B., “EXPOKIT – A Matrix Package for Computing Matrix Exponentials,” ACM Transactions on Mathematical Software, 24 (1998) pp. 130–156. -
LSODA/LSODE solver
The estimated local error for each component, Y(i), is controlled so as to be roughly less (in magnitude) than RTOL*abs(Y(i)) + ATOL. Thus, the local error test passes is, in each component, either the absolute error is less than ATOL or the relative error is less than RTOL. If RTOL is set to 0.0, then only ATOL is applied by the solver (pure absolute error control). Currently, the use of pure relative error control (that is, ATOL is set to 0.0) is not permitted for the LSODE/LSODA solver and can lead to errors. Note that both tolerances are local controls on the current integration interval, and the global error may exceed these values.
For LSODE and LSODA, MAXSTEP is the maximum number of steps allowed during one call to the solver and ‘MAXSTEP = 0’ means that, at most, 5,000 steps will be used.
For a more complete discussion of error controls, see Hindmarsh, Alan C., “ODEPACK, A Systematized Collection of ODE Solvers,” Scientific Computing, R. S. Stepleman et al (eds.), North-Holland, Amsterdam (1983) pp. 55–64. -
DVERK (non-stiff) solver
For the DVERK solver, only relative tolerance (RTOL) applies and serves as a global tolerance term (that is, the ATOL value is ignored): the solver attempts to control a norm of the local error in such a way that the global error is proportional to RTOL. It is worth pointing out that a global tolerance cannot be set to zero.
For this solver, MAXSTEP represents the maximum number of function evaluations allowed during one call to the solver, ‘MAXSTEP = 0’ means that there is no limit in the number of function evaluations.
For a full discussion, see http://www.cs.toronto.edu/NA/Users.Guide.For.DVERK.pdf. -
DOPRI5 (non-stiff) solver
The code keeps the local error of Y(i) below RTOL*abs(Y(i)) + ATOL. Thus, the local error test passes if, in each component, either the absolute error is less than ATOL or the relative error is less than RTOL. If RTOL is set to 0.0, then only ATOL is applied by the solver (pure absolute error control). Similarly, if ATOL is set to 0.0, only RTOL is applied by the solver.
For DOPRI5, MAXSTEP denotes the maximum number of steps allowed during one call to the solver and ‘MAXSTEP = 0’ means that, at most, 100,000 steps will be used.
For a full discussion, see Hairer, Norsett, and Wanner (1993): Solving Ordinary Differential Equations. Nonstiff Problems. 2nd edition. Springer Series in Comput. Math., vol. 8.
