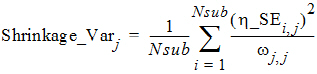Shrinkage calculation

The Omega output worksheet contains h shrinkage data. It is based on the standard deviation definition:

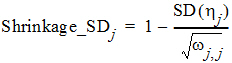
where SD(h_j) is the empirical standard deviation of the j^th h over all Nsub subjects, and w_j,j is the estimate of the population variance of the j^th random effect, j = 1,2,…, NEta.

For all population engines other than QRPEM, the numerical h_j value used in the shrinkage computation is the mode (maximum) of the empirical Bayesian posterior distribution of the random effects h_j, evaluated at the final parameter estimates of the fixed and random effects. For QRPEM, the h_j value is the mean of the empirical Bayesian distribution.

It is worth pointing out that another common way to define the h-shrinkage is through the variance, and is given by

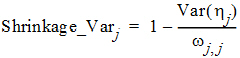
where Var(h_j) is the empirical variance of the j^th h over all Nsub subjects. By the two previous equations, one can see that standard deviation based h-shrinkage can be computed from variance based h-shrinkage, and vice versa. For example, if one has Shrinkage_Var_j, then Shrinkage_SD_j can be calculated as:

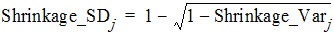
The Eta output worksheet contains the individual shrinkage, which is calculated as follows:

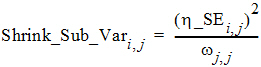
where i = 1, 2, …, Nsub and j = 1, 2, …, NEta. Here, h_SE_i,j denotes the standard error of the j^th individual parameter estimator for the i^th subject. For all population engines other than QRPEM, h_SE_i,j is calculated as the square root of the (j, j)^th element of the inverse of the negative Hessian (second derivative matrix) of the empirical Bayesian posterior distribution for the i^th subject. While, for the QRPEM engine, they are computed via the importance sampling of the empirical Bayesian posterior distribution.

The formula used to calculate Shrink_Sub_Var (the previous equation) is extended from the 1-1 relation between the population shrinkage and standard error of individual parameter estimator conjectured in Xu, et al, AAPS J., (2012) pp. 927-936. This relationship can be intuitively observed from the following important theoretical relationship obtained for the EM algorithm.

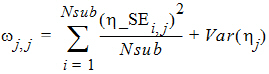
From which, one can see that the commonly used variance based population shrinkage becomes

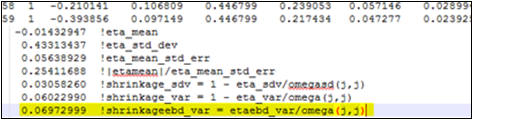
It is worth pointing out that population shrinkage calculated using the above formula is also reported in bluptable.dat (after the individual shrinkages for each h), and is denoted as shrinkageebd_var (see the highlighted text in yellow in the image below). From these results, we can see that the value of shrinkageebd_var is similar to the one for Shrinkage_Var.

In bluptable.dat, Shrink_Sub_SD is calculated by using the following formula

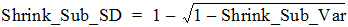
This relationship between Shrink_Sub_SD and Shrink_Sub_Var is an analog of the relationship shown in the earlier Shrinkage_SD equation.