Nonparametric adaptive grid search
Applicable to Gaussian or user-defined likelihood data, nonparametric adaptive grid search (NPAG) is implemented in Phoenix NLME as a post-processor, to be used after one of the parametric engines has been run.
NPAG makes no assumptions regarding the random effects distribution, conceptually modeling the distribution as a discrete distribution on an arbitrarily fine grid in random effects space. It can be used, for example, to detect bimodality in a parameter such as a clearance. In the nonparametric log likelihood function, the parameters to be fit are the probabilities associated with each grid point in the random effects space.
If the grid is very fine, there can be an enormous number of these probabilities. However, mathematically it can be shown that at the maximum likelihood distribution, almost all of the probabilities are zero, which can be used to simplify the computation. The optimal nonparametric distribution takes the form of a discrete distribution on at most N support points, that is, at most N of the probabilities are non-zero, regardless of how many starting grid points were used.
An iteration for the nonparametric engine involves:
Selection of a set of candidate support points, which usually includes all of the support points with non-zero probability from the previous iteration plus generation of some additional candidates that are likely to improve the likelihood of the nonparametric distribution.
Computation of the optimal probabilities on the candidate support points.
The number of iterations to apply is user-specified. On the first iteration, the support points are set at the optimal post-hoc estimates from the initial parametric run. Any fixed effects associated with the residual error model or covariate models are frozen to the values from the parametric run for all of the iterations. A specially designed convex primal dual optimization engine then computes optimal probabilities on these support points.
If subsequent iterations are desired, Phoenix first discards any current iteration support points with a probability of zero, and then introduces additional candidate support points and the primal dual algorithm is reapplied to compute a new discrete distribution, which in general will include at least some of the new candidate support points. From iteration to iteration, the likelihood improves monotonically, and the support points migrate to optimal positions. The Phoenix algorithm has the capability of optimizing both probabilities and support point positions using multiple iterations. The NONMEM nonparametric algorithm can only perform a single pass that optimizes probabilities on support points fixed at POSTHOC estimates from a preceding parametric run.
The primary raw result of the Phoenix nonparametric algorithm is the optimal discrete distribution of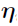 
s in terms of support points and associated probabilities. The means, any covariances, and marginal distributions of each 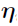of this distribution are reported. In addition to the optimal population distribution, each individual has a discrete posterior distribution from which a mean 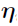value can be computed. Tables of nonparametric 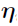means are produced, as are covariate vs. nonparametric 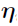mean plots, which can be used to screen for potential covariate relationships.
Note: If the Model engine gives an exception, it is a general exception caused by a bad fit to data. Should an exception occur, try reconsidering the engine, initial parameters estimates, and number of compartments.
How NPAG Works
The NPAG implementation in Phoenix NLME is as an option for post processing, not as an independent engine. This is mostly because the nonparametric method is not as widely used as the parametric methods introduced before, and it is usually slower than parametric methods. This section briefly introduces how NPAG works. Interested users can find more details about NPAG in [4].
When the number of support points K, the location of support points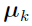 
, and 
are given, finding the weights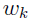 
by maximizing the log-likelihood (or minimizing the negative log-likelihood) is a convex optimization problem and it is relatively easy to solve. In NPAG, the primal-dual interior-point (PDIP) method is used to find the optimal weights 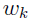. (Note that PDIP is not the only method to find the optimal weights, the method described in [23] can also be used.) Supporting points with very small weights are deleted to ensure K is no more than the number of subjects NSUB. Once the weights 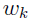are found by PDIP, a BFGS algorithm [24] is used to find (if needed) by maximizing the log-likelihood.
The challenging part is to find the optimal support points 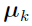. In NPAG, for each of the K support points 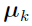, two additional support points are generated along each dimension of the parameter space. For example, if 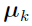has the dimension d, NPAG will generate 2d new support points, including the original 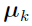, which leads to 2d + 1 support points. So the original K support points will become (2d + 1)K support points. This procedure is called adaptive grid search.
Once the (2d + 1)K support points are obtained, NPAG uses PDIP to find the new optimal K and the corresponding weights 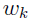, then it finds . Thus, NPAG iterates between the adaptive grid search and PDIP, until the log-likelihood:
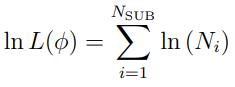
(discussed earlier) stabilizes.