Two-Stage Nonlinear Random Effects Mixture Model
This section describes the mathematics behind a two-stage nonlinear mixture model [3].
Stage One
Given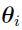 
is the parameter vector describing the unobserved random effects (
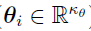), and 
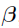describes the unobserved fixed effects (
), then the mi-dimensional observation vector for the ith individual 
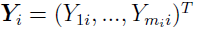is sampled from a Gaussian distribution such that
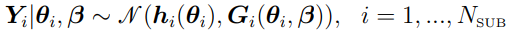
where:
NSUB represents the number of subjects.
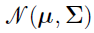is the multivariate Gaussian distribution with mean vector 
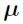and the covariance matrix 
.
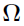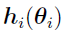is the function defining the PK/PD model.
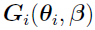is a positive definite covariance matrix (
).
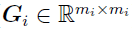Note: This equation is another form of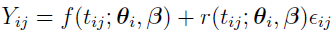 
, discussed in the “Laplacian-Approximation-Based Algorithms” section, where 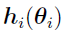replaces 
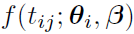, and 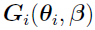replaces the covariance part 
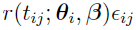. It is used simply for notational convenience in this section.
Consider the case [3]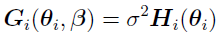 
, where 
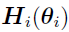is a known function and = 
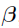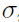2. In this usage, a random effect parameter can change from subject to subject; while a fixed effect parameter is constant over the population.
Stage Two
Each of the NSUB parameter vectors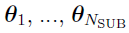 
is sampled from a Gaussian distribution with K mixing components:
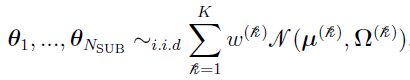
(discussed in “Explore the Formulation of EM ”)
Given the observation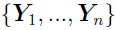 
:
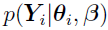can be defined as the likelihood function of 
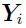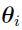given and .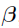
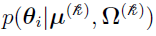can be used to denote the multivariate Gaussian distribution of 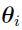, with mean vector 
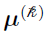and covariance matrix 
.
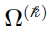Now estimate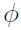 
, which represents the collection of parameters 
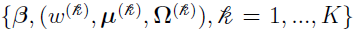, by maximizing the overall data likelihood L(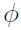) which can be written as
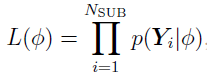
where
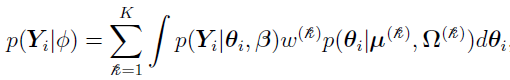
and the multivariate Gaussians are
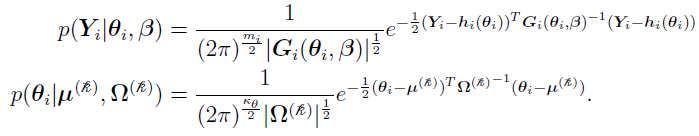
This process is called the maximum likelihood estimate (MLE). The MLE of 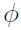is defined as 
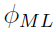such that 
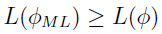for all 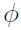within the parameter space.