Iterative Two-Stage – Expectation Maximization (IT2S-EM) was developed around the 1980s [14] and applies to all types of data, including continuous data, modeled with a Gaussian (normal) likelihood, as well as count, categorical, and time-to-event data for which a likelihood function must be specified. IT2S-EM iteratively performs iterative two-stage (IT2S) and EM-like steps, attempting to improve the approximate marginal likelihood at each iteration. It is not a true EM engine. The population mean (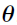
) and residual error (
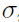) updates follow an iterative two-stage strategy, while the 
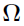update uses an EM strategy. Additionally, unlike true EM, the 
estimates are modes of the joint density, whereas EM uses means.
The iteration sequence is as follows:
Conditional step: for current values of (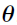, , 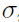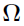), for each individual compute an optimal (also known as an empirical Bayesian or POSTHOC estimate). These s maximize the joint likelihood defined by the product of the distribution of the individual residuals, conditioned on , and the population distribution of s. Algorithms such as IT2S-EM, FOCE L-B, FOCE ELS, Laplacian, and Adaptive Gaussian Quadrature all require performance of this same joint likelihood optimization step and are called 'conditional methods' since the evaluation of the approximate marginal likelihood requires computing model predictions that are conditioned on using the values computed by optimizing the joint likelihood.
In addition, compute covariance (uncertainty) estimates of the s numerically by computing second derivatives of the joint log likelihood function with respect to the s at the optimal values. As a by-product of this computation, the Laplacian approximation to the marginal log likelihood function is obtained for the current (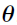, , 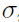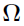) values.
Compute new estimates of 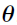and 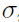given the s by optimizing the joint log likelihood function with respect to (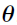, 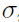) with 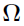and s frozen at current values.
Compute new estimates of 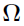from the s and the uncertainties on the s using the standard EM 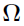update formula.
Usually, the likelihood improves from iteration to iteration, but there is no theoretical guarantee of this happening. The iterations stop based on lack of progress in the log likelihood over several iterations. This can indicate convergence, oscillatory, or even divergent behavior. The best likelihood solution obtained before termination is reported. Since IT2S-EM fit is not an accurate likelihood maximum, standard error results are not reported, as they would also be inaccurate, and possibly not meaningful or even computable.
Often IT2S-EM makes rapid progress during the first few iterations even when the overall sequence of iterates does not converge. A useful strategy regardless of the convergence behavior can be to run a few iterations of IT2S-EM to get an improved starting solution for other engines.
For a more mathematical look at the two-stage portion of IT2S-EM, see “Two-Stage Nonlinear Random Effects Mixture Model”.