Explore the Formulation of AGQ
For the adaptive Gaussian quadrature (AGQ) method, the equation
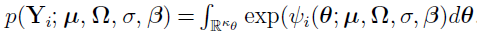
(discussed in “Laplacian Approximation Method and the Resulting Algorithms”) is rewritten as follows
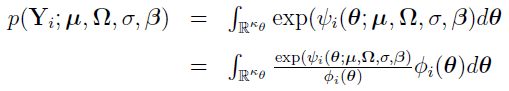
where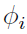 
denotes the PDF of a multivariate normal distribution with mean chosen to be the mode of 
, 
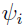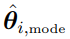, obtained with population parameter 
, 
, 
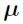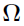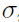and 
, and 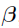covariance matrix being the negative Hessian of 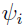at 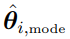. Now apply the Gaussian-Hermite quadrature and obtain:
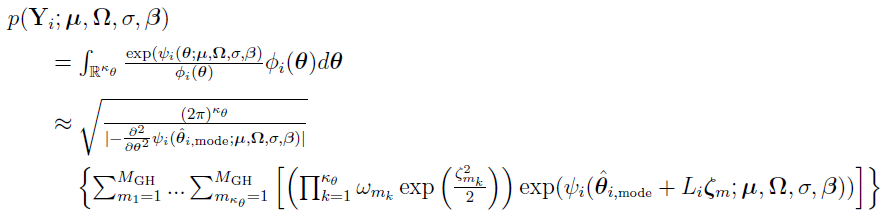
Here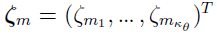 
, 
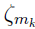is the standard abscissa for one-dimensional Gaussian-Hermite quadrature, and 
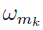denotes the corresponding weight. The matrix Li satisfies that
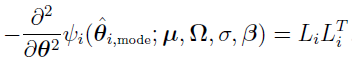
Looking at the earlier equation:
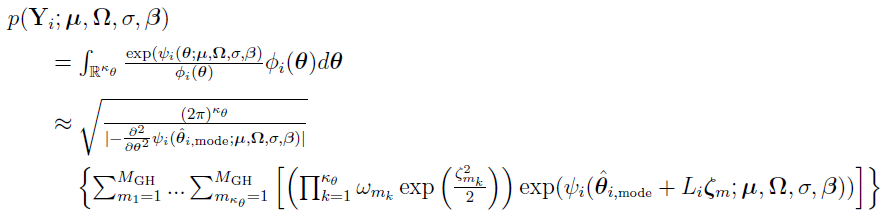
it is observed that the adaptive Gaussian quadrature method also involves a conditional step. It is implemented using the same basic structure as the Laplacian approach. In other words, it also conceptually involves only one top-level optimization problem given by
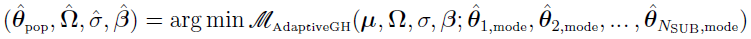
and, at each optimization step, NSUB inner optimization problems need to be done with population parameter estimates obtained at the previous step to evaluate the objective function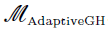 
. The top-level objective function is given by
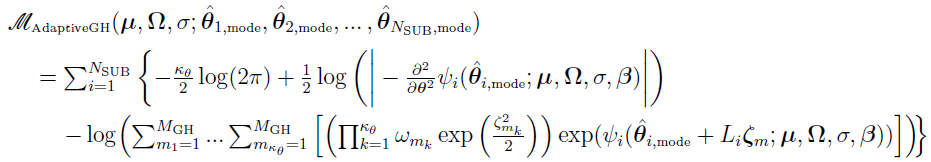
Note that, if only one quadrature point is chosen (i.e., MGH = 1), then the abscissa and weight are respectively given by 0 and 1. Hence, by the previous equation, 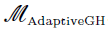reduces to
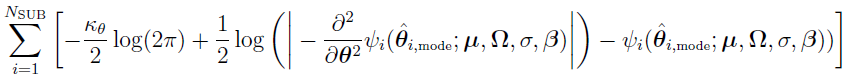
By the above expression and
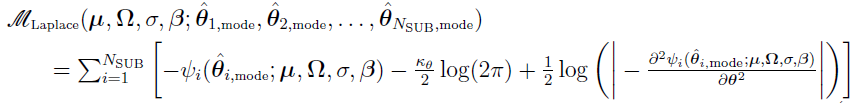
(discussed in “Explore the Formulation of Laplacian”) the objective function for the adaptive Gaussian quadrature method with one quadrature point is exactly the same as the one for the Laplacian method. Thus, the Laplacian method is a special case of the adaptive Gaussian quadrature method.
Compared to linearization and Laplacian methods, the approximate marginal PDF obtained using the adaptive Gaussian quadrature method can be made arbitrarily close to the true one. However, it suffers the curse of dimensionality, and hence is often most useful for improving estimation accuracy for models with small numbers of random effects. As the adaptive Gauss quadrature rule does not rely on any assumption on the residual errors, it is applicable to both Gaussian and non-Gaussian data.