The ordinary differential equation (ODE) is defined in PML through the deriv statement. The following example demonstrates the syntax for defining a population PK model through ODEs.
1 mymodel(){
2 ## STRUCTURAL MODEL SECTION
3 deriv(aa=-aa*ka)
4 deriv(a1=aa*ka-a1*cl/v)
5 dosepoint(aa)
6 c=a1/v
7 ## PARAMETER MODEL SECTION
8 stparm(
9 ka=tvKa*exp(nKa)
10 cl=tvCl*exp(nCl)
11 v=tvV*exp(nV)
12 )
13 fixef(
14 tvKa=c(, 10,)
15 tvCl=c(, 5,)
16 tvV=c(, 8,)
17 )
18 ranef(
19 diag(nKa, nCl, nV)=c(1.0, 0.5, 0.6)
20 )
21 ## ERROR MODEL SECTION
22 error(eps1=0.01)
23 observe(cObs=c+eps1)
24 }Lines 1–24 define a model called “mymodel.” It is a one-compartment model with first-order absorption and is parameterized by clearance and volume. The model statements can be grouped into sections for structural, parameter, and error models. The model contains several user-defined and reserved names.
Line 3 gives the differential equation for the absorption compartment. It is read as “the derivative of aa is -aa*ka.” The variable aa represents the amount of the drug in the absorption compartment.
Line 4 gives the differential equation for amount in the central compartment, a1.
Note: PML works best when the right-hand side of each differential equation has no time-discontinuities. An example of a system which is time-discontinuous is:
deriv(a1=-a1*cl/v)
cl=(t<t1 ? cl1:cl2)
This is time-discontinuous because clearance jumps at time t1 from cl1 to cl2 and it appears on the right-hand-side of the differential equation for a1. This has the effect of causing the ODE solver to step back and forth over time t1, in ever smaller steps, attempting to reduce its error. It is much better to use the sequence statement (explained in the “Action code” and “The sequence and sleep statements” sections), which can run the ODE solver up to particular times (called change points), then perform some discontinuous modifications to the model and run the ODE solver forward again. In fact, if Matrix Exponent is requested, it will not run this code. It will switch to a different solver because it requires that the system be not only continuous, but linear between change points. See “Matrix Exponent” for more information about this method.
Thus, the use of t, representing time since the subject began processing, is what is used in the above manner, is discouraged.
It is worth pointing out that, if the initial condition for an ODE is non-zero (such as the case for the indirect response model), then it can be specified through the sequence statement (see “The sequence and sleep statements” for details).
Line 5, the dosepoint statement, says that aa, the absorption compartment, can receive doses. If the central compartment can also take doses, the model can include an additional dosepoint statement. For more information, see the “Dosing” section.
Line 6 is a simple assignment statement saying that concentration c in the central compartment is equal to the amount in the central compartment a1 divided by volume v. This quantity is related to the observed quantity in line 23. Assignment statements are performed in the order that they are displayed in the model.
Lines 8–12 identify the structural parameters and their associations with the fixed and random effects. If a model is used for single-subject estimation, only the fixed effects are estimated. The model can include any number of stparm statements. Structural parameter statements should only include fixed effects, random effects, and covariates. They should not include variables that are evaluated as assignment statements. Structural parameter statements are executed before anything else and are only re-executed during a given iteration if a covariate changes, so any variables from assignment statements will be undefined on the initial execution of the stparm statements, possibly leading to model failure. For more information, see “Structural parameters and group statements”.
Lines 13–17 identify the population fixed effect parameters (Thetas). It is recommended that a consistent naming convention is used to make the model more easily understood by others. In this example, variables representing typical values start with the letters “tv,” followed by a capitalized variable name, such as tvCl for clearance or tvV for volume. The model can include any number of fixef statements.
After each fixed effect is an optional assignment, providing either a single number representing the initial value of the parameter or a list of three numbers representing a lower bound, an initial value, and an upper bound, in that order.
If the assignment is used, then the initial estimate must be provided. The lower and upper bound values can be omitted but the order must be maintained by using blank spaces and commas as delimiters. The correct syntax is:
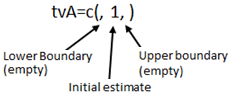
If one value is provided it is assumed that the lower and upper boundaries are not being supplied but the syntax must be correct. For example, tvA=c(1) does not work. However, omit the parenthesis and use tvA=1, and the PML assumes that one is the initial value assigned to the parameter.
See the “Fixed effects” section for more information.
Lines 18–20 define the variance-covariance matrix of the random effects (i.e., Omega). In this model, there are three random effect variables, nKa, nCl, nV, grouped into a single block. The diag means that the Omega matrix is a diagonal matrix with initial values given as a list of numbers through c. Multiple blocks are supported. The model can include any number of ranef statements. For more information, see the “Random effects” section.
Line 22 identifies that there is an observational error variable (epsilon) called eps1, and the initial estimate for the standard deviation of eps1 is given as 0.01. Supplying the initial estimate of standard deviation is optional. If it is not provided, a value of 1 is used. Models can include multiple error variables but only one per observe statement.
Line 23 specifies the observed quantity cObs and says it is equal to the predicted concentration c plus the error variable. The expression must contain one and only one error variable. Various PK and PD error models can be expressed in this way.
Only a single error variable can be used in an observe statement such as the one on line 23. Compound residual error models for any given observed variable, such as mixed additive and proportional, must be built using a combination of fixed effects and a single error variable rather than multiple error variables. For example, the following statements are correct:
stparm(CMixRatio = tvCMixRatio)
fixef(tvCMixRatio = c(, 0.1, ))
error(eps1 = 0.01)
observe(cObs = c + eps1*(1 + c*MixRatio))
The following statements are incorrect as the observe statement contains two error variables, eps1 and eps2:
error(eps1 = 0.01)
error(eps2 = 0.001)
observe(cObs = c*(1 + eps2) + eps1)
For more information on the observe statement, see the “Observations” section.