Population modeling run options
The following options are displayed in the Run Options tab when the Population? box is checked.
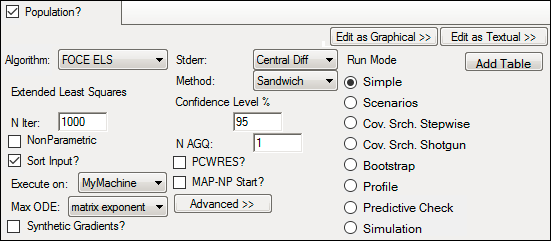
Not all run options are applicable for every run method. Some options are made available or unavailable depending on the selected run method. For detailed explanations of Maximum Likelihood Models run options, see the “Run modes” section.
In the Algorithm menu, select a run method:
FOCE L-B (First-Order Conditional Estimation, Lindstrom-Bates)
FOCE ELS (FOCE Extended Least Squares)
FO (First Order)
Laplacian
Naive pooled
IT2S-EM (Iterated two-stage expectation-maximization)
QRPEM (Quasi-Random Parametric Expectation Maximization)
In the N Iter field, type the maximum number of iterations to use with each modeling run (the default is 1000).
Check the NonParametric box to use the NonParametric engine for producing nonparametric results in the output.
If selected, type the maximum number of iterations of nonparametric computations to complete during the modeling process in the N NonPar field.
Available for FOCE L-B, FOCE ELS, Laplacian, IT2S-EM, and QRPEM methods.
Check the Sort Input? box to sort the input by subject and time values. (Refer to the Sort Input? description in the Individual Modeling section for additional information.)
Select the local or remote machine or grid on which to execute the job from the Execute on menu.
The contents of this menu can be edited, refer to the “Compute Grid preferences” section.
Note: When a grid is selected, loading the grid can take some time and it may seem that the application has stopped working.
Make sure that you have adequate disk space on the grid for execution of all jobs. A job will fail on the grid if it runs out of disk space.
From the Max ODE menu, select one of the ODE (ordinary differential equations) solver methods. For more on ODE methodology, see the “Differential Equations in NLME” section.
Check the Synthetic Gradients? box to allow synthetic gradients in the model.
When this is selected in population modeling, the engine computes and makes use of analytic gradients with respect to etas. In some cases, with differential equation models, one or more gradient components can be computed by integrating the sensitivity equations along with the original model system using a numerical differential equation solver. For reasonably sized models, selecting Synthetic Gradients can help speed and accuracy.
Select the Method for computing the covariance matrix of parameter estimators:
Standard errors of parameter estimators are computed as the square roots of diagonal elements of the covariance matrix of parameter estimators. The covariance matrix is evaluated using the Hessian method and is computed as the inverse of the Hessian matrix (matrix of second-order partial derivatives) of the negative log-likelihood function with respect to estimated parameters.
Fisher Score: Evaluates the covariance matrix as the inverse of the score matrix (S), which is defined as the sum of outer product of the gradient (vector of first-order partial derivatives) of each individual’s log-likelihood function with respect to estimated parameters. The Fisher Score method is fast and robust, but less precise than the Sandwich and Hessian methods.
Hessian: The covariance matrix is the inverse of the Hessian matrix (H) of the negative log-likelihood function with respect to estimated parameters. This is the only method available for individual models.
Sandwich: Evaluates the covariance matrix as H-1SH-1. The Sandwich method has both advantages and disadvantages relative to the Hessian method. The main advantage is that, in simple cases, the Sandwich method is robust for covariance model misspecification, but not for mean model misspecification. The main disadvantage is that it can be less efficient than the simpler Hessian method when the model is correctly specified.
Auto-detect: When selected, NLME chooses the method. Specifically, if both Hessian and Fisher score methods are successful, then it uses the Sandwich method. Otherwise, it uses either the Hessian method or the Fisher Score method, depending on which method is successful. Check the Core Status text output to see which method is used.
In the Confidence Level % field, enter the confidence interval percentage.
From the Finite Difference Method menu, select the form of standard error to compute.
none: No standard error calculations are performed.
Central Diff: The second-order derivative of f uses the form:
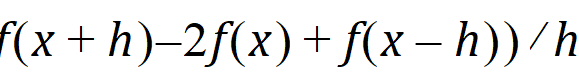
Forward Diff: The second-order derivative of f uses the form:
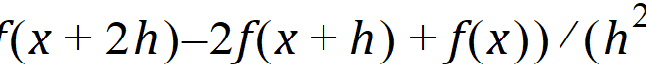
Note: Computing the standard errors for a model can be done as a separate step after model fitting. This allows reviewing of the model fitting results before spending the time computing standard errors.
For engines other than QRPEM:
– After doing a model fitting, accept all final estimates of the fitting.
– Set the number of iterations to zero.
– Rerun with a method selected for the Finite Difference Method option.
For QRPEM, use the same steps, but also request around 15 burn-in iterations.
In the N AGQ field, enter the maximum number of integration points for the Adaptive Gaussian Quadrature.
Available for FOCE ELS and Laplacian methods.
In the ISAMPLE field, enter the number of sample points or use the default.
For each subject, the joint likelihood, the mean, and the covariance integrals will all be evaluated with this number of samples from the designated importance sampling distribution. Increasing this number improves the accuracy of the integrals. This option is available for the QRPEM method.
Check the PCWRES? box to generate the predictive check weighted residuals in the results.
When checked, enter the number of replicates the nrep field or use the default. The maximum number of replicates is 1001, a number higher than this is automatically reduced, by the system, to 1001 and a warning appears in the Core Status tab.
Available for FOCE L-B, FOCE ELS, FO, Laplacian, and IT2S-EM methods. PCWRES is an adaptation of France Mentre’ et al.'s normalized predictive error distribution method. Each observation for each individual is converted into a nominally normal N(0,1) random value. It is similar to WRES and CWRES but computed with a different covariance matrix. The covariance matrix for PCWRES is computed from simulations using the time points in the data.
Check the MAP-NP Start? box to perform Maximum A Posteriori initial Naive Pooling.
If selected, enter the number of iterations to apply MAP-NP in the Iterations field.
Available for FOCE L-B, FOCE ELS, FO, Laplacian, QRPEM and IT2S-EM methods.
This process is designed to improve the initial fixed effect solution with minor computational effort before a main engine starts. It consists of alternating between a Naive pooled engine computation, where the random effects (etas) are fixed to a previously computed set of values, and a MAP computation to calculate the optimal MAP eta values for the given fixed effect values that were identified during the Naive Pooled step.
On the first iteration, MAP-NP applies the standard Naive pooled engine with all etas frozen to zero to find the maximum likelihood estimates of all the fixed effects. The fixed effects are then frozen and a MAP computation of the modes of the posterior distribution for the current fixed effects parameters is then performed. This cycle of a Naive pooled followed by MAP computation is performed for the number of requested iterations. Note that, throughout the MAP-NP iteration sequence, the user-specified initial values of an eps and Omega are kept frozen.
Check the FOCEHess? box to use FOCE Hessian.
Available for Laplacian and IT2S-EM methods.
Advanced options
1. Press Advanced to toggle access to advanced run options for population models (only).
All engines have the following Advanced options.
2. In the LAGL nDig field, enter the number of significant decimal digits for the LAGL algorithm to use to reach convergence.
Available for FOCE ELS and Laplacian methods.LAGL, or LaPlacian General Likelihood, is a top-level log likelihood optimization that applies to a log likelihood approximation summed over all subjects.
2. In the SE Step field, enter the standard error numerical differentiation step size.
Available for all run methods except IT2S-EM, which does not compute standard errors. SE Step is the relative step size to use for computing numerical second derivatives of the overall log likelihood function for model parameters when computing standard errors.
3. In the BLUP nDig field, enter the number of significant decimal digits for the BLUP estimation to use to reach convergence.
Available for all run methods except Naive-Pooled. BLUP, or Best Linear Unbiased Predictor, is an inner optimization that is done for a local log likelihood for each subject. BLUP optimization is done many times over during a modeling run.
4. In the Model Linearization Step Size field, enter the model linearization numerical differentiation step size.
Available for the FOCE ELS and FOCE L-B methods, the IT2S-EM method (when applied to models with Gaussian observations), and the Laplacian method (when the FOCEhess option is selected and the model has Gaussian observations).
Model Linearization Step Size is the step size used for numerical differentiation when linearizing the model function in the FOCE approximation.
5. In the ODE Rel. Tol. field, enter the relative tolerance value for the ODE solver.
6. In the ODE Abs. Tol. field, enter the absolute tolerance value for the ODE solver.
7. In the ODE Max Step field, enter the maximum number of steps for the ODE solver.
QRPEM advanced options
The following are additional advanced options available only for the QRPEM method.
1. Check the MAP Assist box to perform a maximization of the joint log likelihood before each evaluation of the underlying integrals to find the mode.
If checked, enter the period in the field. (For example, a value of two specifies that MAP assist should be used every other iteration.)
The importance sampling distribution is centered at this mode value. If MAP Assist is not checked, the mode finding optimization is only done on the first iteration and subsequent iterations use the mean of the conditional distribution as found on the previous iteration.
2. In the Acceptance Ratio field, enter a decimal value for the acceptance ratio.
The default is 0.1. As this value is reduced below 0.1, the importance sampling distribution becomes broader relative to the conditional density.
3. Select the importance sampling distribution type from the Imp Samp Type menu.
normal: Multivariate normal (MVN)
direct: Direct sampling
double-exponential: Multivariate Laplace (MVL): The decay rate is exponential in the negative of the sum of absolute values of the sample components. The distribution is not spherically symmetric, but concentrated along the axes defined by the eigenvectors of the covariance matrix. MVL is much faster to compute than MVT.
T: Multivariate t (MVT): The decay rate is governed by the degrees of freedom: lower values correspond to slower decay and fatter tails.
If selected, enter the Number of Degrees of Freedom in the field. A value between four and 10 is recommended, although any value between three and 30 is valid.
mixture-2: Two-component defensive mixture. (See T. Hesterberg, “Weighted average importance sampling and defensive mixture distributions,” Tech. report no. 148, Division of Biostatistics, Stanford University, 1991). Both components are Gaussian, have equal mixture weights of 0.5, and are centered at the previous iteration estimate of the posterior mean. Both components have a variance covariance matrix, which is a scaled version of the estimated posterior variance covariance matrix from the previous iteration. One component uses a scale factor of 1.0, while the other uses a scale factor determined by the acceptance ratio.
mixture-3: Three-component defensive mixture. Similar to the two-component case, but with equal mixture weights of 1/3 and scale factors of 1, 2, and the factor determined by the acceptance ratio.
Note: ISAMPLE, Imp Samp Type, and Acceptance Ratio can all be used to increase or decrease the coverage of the tails of the target conditional distribution by the importance sampling distribution.
4. Select the Quasi-Random scrambling method to use from the Scramble menu: None, Owen, or TF.
5. In the # SIR Samp field, enter the number of samples per subject used in the Sampling Importance Re-Sampling algorithm to determine the number of SIR samples taken from the empirical discrete distribution that approximates the target conditional distribution.
The number of SIR samples from each subject are merged to form the basis for a log-likelihood optimization that allows fixed effects that are not paired with random effects to be estimated. The number of samples is usually far smaller than the number that would be used if the SIR algorithm were not used.
The default of 10 is usually adequate, unless the number of subjects is extremely small. If necessary, the number of SIR samples can be increased to a maximum of ISAMPLE.
6. In the # burn-in Iters field, type the number of QRPEM burn-in iterations to perform at startup to adjust certain internal parameters.
During a burn-in iteration, importance sampling is performed and the three main integrals are evaluated, but no changes are made to the parameters to be estimated or the likelihood. The default is zero, in which case the QRPEM algorithm starts normally. Typical values, other than zero, are 10 to 15.
7. Check the Frozen omega burn-In box to freeze the omega but not theta for the number of iterations entered in the # burn-in Iters field.
If this is not checked, then both omega and theta are frozen during the burn-in.
8. Check the MCPEM box to use Monte-Carlo sampling instead of Quasi-Random.
Although Quasi-Random is recommended, using Monte-Carlo sampling may be necessary if the most direct comparison possible with other MCPEM algorithms is desired.
9. Check the Run all box to ignore the convergence criteria and run all iterations.