[Click inside a blue square in the image to jump to the corresponding description.]
Use the Parameterization pulldown to select the type of parameterization for the model. Each parameterization option changes the parameters and statements listed.
Micro: Expresses the model as differential equations having mass transfer rate constants associated with a compartmental model. Adds the mass transfer rate parameters, such as Ke, the rate of elimination, and writes the derivatives in terms of compartmental masses.
Clearance: Expresses the model as differential equations having clearances associated with a compartmental model. Adds the inter-compartmental clearance parameters, such as Cl, the clearance rate. If Clearance is selected, checking the Saturating box converts the model to a saturable elimination (Michaelis-Menten kinetics) model. A saturable model uses two parameters:
Km: Concentration to achieve half of maximal metabolic rate.
Vmax: The maximum metabolic rate.
Macro: Expresses the model as a closed-form sum of exponentials. This option directly models concentration in the central compartment. Primary parameters are the sum of exponential terms that model concentration in the central compartment. Volume is not in the model but can be derived as a secondary parameter.
The Macro model has a sum of exponentials that are fitted to the original observed value of C, using some original dose, called the “stripping dose.” If the model is again fitted against data obtained at another time with a higher or lower dose, then the question is how to make the model predict higher or lower values of C. This is done by multiplying the model's predicted value of C by a ratio of the current dose and the original dose. Enter the dose (A1) as well as a stripping dose (A1Strip). If no stripping dose is mapped, the stripping dose is assumed equal to the dose.
Macro1: Model is expressed as a closed-form sum of exponentials. This option models the amount in the central compartment (A) and Volume is a primary parameter. Primary parameters are the sum of exponential terms plus the parameter Volume. The amount in the central compartment is modeled as a sum of exponentials and then the Volume parameter is used to convert that amount to a concentration. Note that, because both macro options are closed-form models, the Closed form? option is removed.
For Micro or Clearance parameterization, check the Closed form box to convert the model from a differential equation model to a closed-form algebraic model.
The closed-form model runs faster, but has some disadvantages:
There can only be one observed variable.
The differential system being converted must be linear.
Any covariates used in the model must be constant for the duration of the observations.
Check the Infusion possible? box if the model uses a constant rate of drug delivery.
Infusions can be selected for intravenous and extravascular input. Selecting this option adds an extra context for the rate of drug delivery to the Main Mappings panel (A1 Rate for intravenous, Aa Rate for extravascular absorption). If checked, use the Duration? checkbox to switch from infusion rate (unchecked) to infusion duration (checked). Note that checking the Duration box changes the context labels from A1/Aa Rate to A1/Aa Duration.
Check the tlag box to add a time delay parameter to the model.
Adding a time lag assumes that there is a fixed amount of time between drug delivery (dose time) and when the drug is introduced into the blood.
Check the Elim. Cpt. box if urine is being analyzed or data is available for any type of elimination compartment.
Selecting this option adds a differential equation for A0, the amount of a drug excreted from the body. An elimination compartment is added to the model and included in the model code as a urinecpt statement. The urinecpt statement is like the deriv statement, except in a steady-state dosing situation, where urinecpt is ignored.
Adding an elimination compartment to a Clearance model removes the Closed form option and adds the Fe? option for toggling the inclusion of the fraction excreted parameter.
In the Absorption menu, select the method of drug delivery or the type of absorption delay.
Intravenous: The drug is introduced directly into the blood.
First-Order: Extravascular administration with the absorption assumed to be first-order. The Ka parameter (rate of absorption) is added along with an extra checkbox to set the rate of absorption equal to the rate of elimination.
Gamma: Extravascular administration with delay time between drug administration and when drug molecules reach the central compartment assumed to be gamma distributed.
Inverse Gaussian: Extravascular administration with delay time assumed to be inverse Gaussian distributed.
Weibull: Extravascular administration with delay time assumed to be Weibull distributed.
The Gamma, Inverse Gaussian, and Weibull options are available only when Clearance or Micro is chosen for parameterization. Selecting any of these three absorption options removes the Closed form? option and adds two extra parameters to the model to characterize the distribution of the absorption delay time (see “The delayInfCpt statement” section in the PML documentation for more information).
Check the Ka = Ke box (available when Micro is chosen for parameterization) to set the absorption rate equal to the elimination rate (the Ke parameter is removed from the model).
From the Num Compartments menu, select the number of compartments.
The default is one central compartment, and up to two peripheral compartments can be added. For each peripheral compartment added, two parameters are added to the model to account for the flow between the compartments.
For Macro parameterization, use the Num Terms menu to set the number of exponential terms to use in the model.
The following parameters are added to the model for each extra compartment or term.
Number | Micro | Clearance | Macro | Macro1 |
|---|---|---|---|---|
1 Comp/Term | V, Ke | V, Cl | A, Alpha | V, Alpha |
2 Comp/Terms | K12, K21 | V2, Cl2 | B, Beta | B, Beta |
3 Comp/Terms | K13, K31 | V3, Cl3 | C, Gamma | C, Gamma |
Select the Sequential PK/PD? checkbox if the PK model is part of a PK/PD model that is being fitted sequentially. This will freeze the PK portion of the model and turn its random effects into covariates. See the “Sequential PK-PD population model fitting” section for more information.
Refer to the “Residual error model options” section for descriptions of the Residual Error fields.
Press Set WNL Model to run Least-Squares Regression model structures using Phoenix NLME.
a. In the first unlabeled menu, select one of the 19 PK models, or one of the four Michaelis-Menten models, or one of the 19 PK/PD simultaneous link models.
The PK/PD simultaneous link models are labeled 401 to 419 and link PK models 1 through 19 with PD model 105 (e.g., PK/PD model 407 is a linked model of PK model 7 with PD model 105). For more on PK/PD simultaneous link models, see the “Differential Equations in NLME” section.
b. If the model specified in the first unlabeled menu is not a macro-parameterization model, check the CL/V box to add clearance and volume parameters to the model.
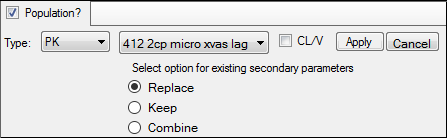
c. If a linked model is specified in the first unlabeled menu, use the second unlabeled menu to choose one of eight PD models, or one of four Indirect Response models to link.
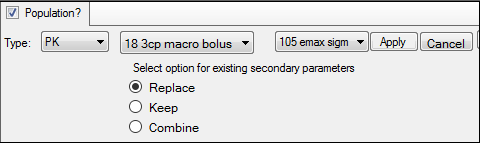
d. Indicate what should be done with secondary parameters that are already defined in the interface when the model is loaded.
Replace currently defined parameters with those from the model.
Keep currently defined parameters and ignore those from the selected model.
Combine the parameters by keeping the existing parameters and adding those from the selected model to the list.
e. Press Apply to accept the selected model(s) or press Cancel to exit the model selection menus without applying any changes.