The Linear Mixed Effects object creates several output worksheets in addition to a text file that lists the model settings. The specific output created depends on the options set in the Linear Mixed Effects object.
For more on how the Linear Mixed Effects object creates output, see the “Linear mixed effects computations” section.
The Output Data section in the Results tab contains linear mixed effects output in worksheet format. The worksheets that are created depends on which model options are selected. All possible worksheets are listed below. For a comprehensive explanation of results worksheets, see the “Output explanations” section.
Contrasts: Hypothesis, df, F-statistic, and p-value.
Contrasts Coefficients: Shows the actual coefficients used in the contrasts.
Diagnostics: Model-fitting information.
Estimates: Estimate, standard error, t-statistic, pvalue, and interval.
Estimates Coefficients: Shows the actual coefficients used in the estimates.
Final Fixed Parameters: Estimates, standard error, t-statistic, p-value, and intervals.
Final Variance Parameters: Estimates and units of the final variance parameters.
Initial Variance Parameters: Initial values for variance parameters.
Iteration History: Data on the variable estimation in each iteration.
Least Squares Means: Least squares means, standard error, df, t-statistic, p-value, and interval.
LSM Coefficients: Shows the actual coefficients used in the least squares means test.
LSM Differences: Shows the differences of intervals and LSMs.
Parameter Key: Information about the variance structure.
Partial SS: Similar to Partial Tests but includes SS and MS.
Partial Tests: Tests of fixed effects but each term is tested last.
Residuals: Dependent variable(s), units, observed and predicted values, standard error and residuals.
Sequential SS: Similar to Sequential Tests but includes SS and MS.
Sequential Tests: Tests of fixed effect for significant improvement in fit, in sequence. Depends upon the order that model terms are written.
User Settings: Information about model settings.
The Linear Mixed Effects object creates two types of text output: a Settings file that contains model settings, and an optional Core Output file. The Core Output text file is created if the Core Output box is checked in the General Options tab. The file contains a complete summary of the analysis, including all output as well as analysis settings and any errors that occur.
The following sections provide more detail about the Linear Mixed Effects object’s worksheet output, including how the results are derived.
Sequential SS and Partial SS worksheets
Residuals worksheet and predicted values
Final fixed parameters estimates
The tests of hypotheses are the mixed model analog to the analysis of variance in a fixed model. The tests are performed by finding appropriate L matrices and testing the hypotheses H0: Lb=0 for each model term.
If an additional test was requested for a model with only fixed effects, the test is performed by computing the ratio of the MS values of the specified fixed effects terms for numerator and denominator. There are no checks to verify the validity of a test, LinMix assumes it is valid.
The Sequential Tests worksheet is created by testing each model term sequentially. The first model term is tested to determine whether it should enter the model. Then the second model term is tested to determine whether it should enter the model, given that the first term is in the model. Then the third model term is tested to determine whether it should enter the model, given that the first two terms are in the model. The model term tests continue until all model terms are exhausted.
The tests are computed using a QR factorization of the XY matrix. The QR factorization is segmented to match the number of columns that each model term contributes to the X matrix.
The Partial Tests worksheet is created by testing each model term given every other model term. Unlike sequential tests, partial tests are invariant under the order in which model terms are listed in the Fixed Effects tab. Partial tests factor out of each model term the contribution attributable to the remaining model terms.
This is computed by modifying the basis created by the QR factorization to yield a basis that more closely resembles that found in balanced data.
Sequential SS and Partial SS worksheets
For models with only fixed effects, the Sequential Tests and Partial Tests are also presented in a form that includes SS (Sum of Squares) and MS (Mean Square).
For fixed effects models, certain properties can be stated for the two types of ANOVA. For the sequential ANOVA, the sums of squares are statistically independent. Also, the sum of the individual sums of squares is equal to the model sum of squares; which means the ANOVA represents a partitioning of the model sum of squares. However, some terms in ANOVA may be contaminated with undesired effects. The partial ANOVA is designed to eliminate the contamination problem but the sums of squares are correlated and do not add up to the model sums of squares. The mixed effects tests have similar properties.
Akaike Information Criterion (AIC)
The Linear Mixed Effects object uses the smaller-is-better form of Akaike’s Information Criterion:
AIC = –2LR + 2s
where:
LR is the restricted log-likelihood function evaluated at the final fixed parameter estimates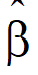 
and the final variance parameter estimates 
.
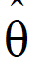s is the rank of the fixed effects design matrix X plus the number of parameters in q (i.e., s = rank(X) + dim(q)).
Schwarz Bayesian Criterion (SBC)
The Linear Mixed Effects object uses the smaller-is-better form of Schwarz’s Bayesian Criterion:
SBC = –2LR + slog(N – r)
where:
LR is the restricted log-likelihood function evaluated at the final estimates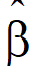 
and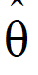 
.
N is the number of observations used.
r is the rank of the fixed effects design matrix X.
s is the rank of the fixed effects design matrix X plus the number of parameters in q (i.e., s = rank(X) + dim(q)).
Note: AIC and SBC are only meaningful during comparison of models. A smaller value is better, negative is better than positive, and a more negative value is even better.
Hessian eigenvalues
The eigenvalues are formed from the Hessian of the restricted log likelihood. There is one eigenvalue per variance parameter. Positive eigenvalues indicate that the final parameter estimates are found at a maximum.
Residuals worksheet and predicted values
In the Linear Mixed Effects object, predicted values for the dependent variables are computed at all of the input data points. To obtain predicted values for data points other than the observed values, supply the desired points in the input dataset with missing dependent variables. Predicted values are estimated by using the rows of the fixed effects design matrix X as the L matrices for estimation, and therefore the predicted values for the input data are equal to:
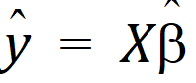
where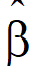 
are the final fixed parameters estimates.
If a log-transform is selected, then the predicted values are also transformed. The residuals are then the observed values minus the predicted values, or in the case of transforms, the residuals are the transformed values minus the predicted values. The variance of the prediction is as follows:
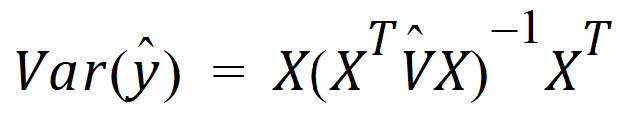
The standard errors are the square root of the diagonal of the matrix above. T-type intervals for the predicted values are also computed.
The Lower_CI and Upper_CI are the bounds on the predicted response. The level is selected in the Fixed Effects tab of the Linear Mixed Effects object.
Final fixed parameters estimates
In the Linear Mixed Effects object, the final fixed effects parameter estimates are computed by solving:
T00b = y0
where:
T00 and y0 are elements of the reduced data matrix as defined in the section on “Restricted maximum likelihood”.
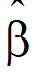are the final fixed parameters estimates.
When there are multiple solutions, a convention is followed such that if any column of T00 is a linear combination of preceding columns, then the corresponding final fixed parameters estimate element is set to zero.
If Show Coefficients is selected on any tab in the Linear Mixed Effects object, then the coefficients of the parameters used to construct the linear combination is displayed in the output. If the linear combination is estimable, then the coefficients are the same as those entered. If the linear combination is not estimable, then the estimable replacement is displayed. This provides the opportunity to inspect what combination is actually used to see if it represents the intentions.
This worksheet lists the fitting algorithm results. If the initial estimates are the REML estimates, then zero iterations are displayed.
If the model includes random or repeated effects, the Parameter column in the Parameter Key worksheet contains the variance parameter names assigned by the Linear Mixed Effects object. If the Group option is not used in the model or if there is only one random or repeated model, then indices are not used in the parameter names.
Otherwise, two indices are appended to the variance parameter names in order to clarify which random or repeated model, or group, the variance parameter addresses. The first index indicates the random model or repeated model to which the parameter applies. An index of 1 indicates the model on the Random 1 tab in the Variance Structure tab. The highest index indicates the repeated model if there was one. The second index is the group index indicating that the parameters within the same group index are for the same group level.
Source: Random if the parameter is from a random model. Repeated if the parameter is from a repeated specification. Assumed if the variance parameter is the residual.
Type: User-specified variance type, or Identity, if the residual variance.
Bands: Number of bands or factors if appropriate for the variance type.
Subject_Term: Subject term for this variance structure, if there was a subject.
Group_Term: Group term for this variance structure, if there was a group.
Group_Level: Level of the group that this parameter goes with, if there was a group.