For linear mixed effects models that contain random effects, the first step in model analysis is determining the maximum likelihood estimates of the variance parameters associated with the random effects. This is accomplished in LinMix using Restricted Maximum Likelihood (REML) estimation.
The linear mixed effects model described in the “General linear mixed effects model” section is:
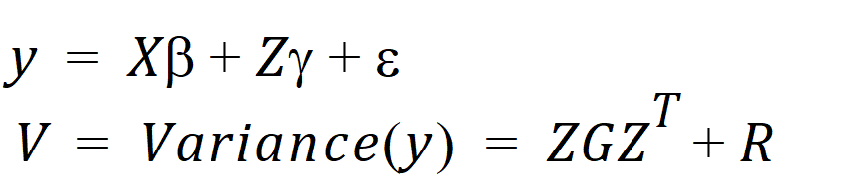
Let q be a vector consisting of the variance parameters in G and R. The full maximum likelihood procedure (ML) would simultaneously estimate both the fixed effects parameters b and the variance parameters q by maximizing the likelihood of the observations y with respect to these parameters. In contrast, restricted maximum likelihood estimation (REML) maximizes a likelihood that is only a function of the variance parameters q and the observations y, and not a function of the fixed effects parameters. Hence for models that do not contain any fixed effects, REML would be the same as ML.
To obtain the restricted likelihood function in a form that is computationally efficient to solve, the data matrix [X | Z | y] is reduced by a QR factorization to an upper triangular matrix. Let [R0 | R1 | R2] be an orthogonal matrix such that the multiplication with [X | Z | y] results in an upper triangular matrix:
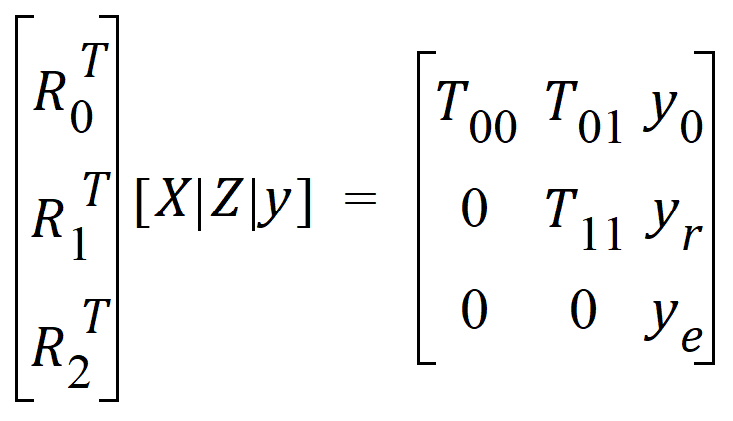
REML estimation maximizes the likelihood of q based on yr and ye of the reduced data matrix, and ignores y0. Since ye has a distribution that depends only on the residual variance, and since yr and ye are independent, the negative of the log of the restricted likelihood function is the sum of the separate negative log-likelihood functions:
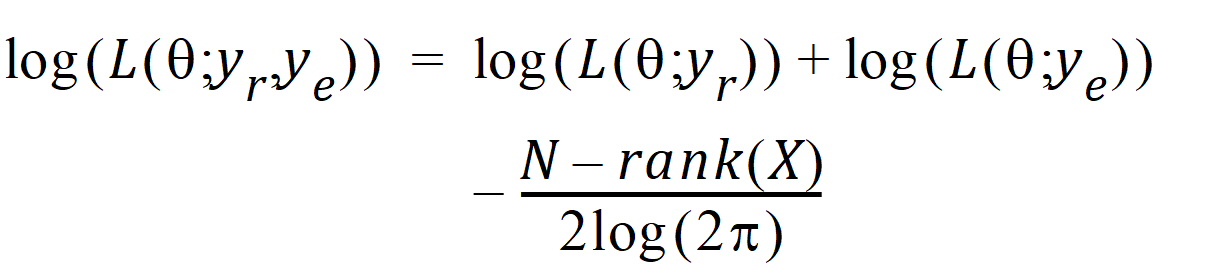
where:
log(L(q; yr)) = –½ log (|Vr |) – ½ yr T Vr –1 yr
log(L(q; ye))=–ne/2 log(qe) – ½ (yeTye/qe)
Vr is the Variance(yr)
qe is the residual variance
ne is the residual degrees of freedom
N is the number of observations used
For some balanced problems, ye is treated as a multivariate residual: [ye1 | ye2 | ... | yen]
in order to increase the speed of the program and then the log-likelihood can be computed by the equivalent form:
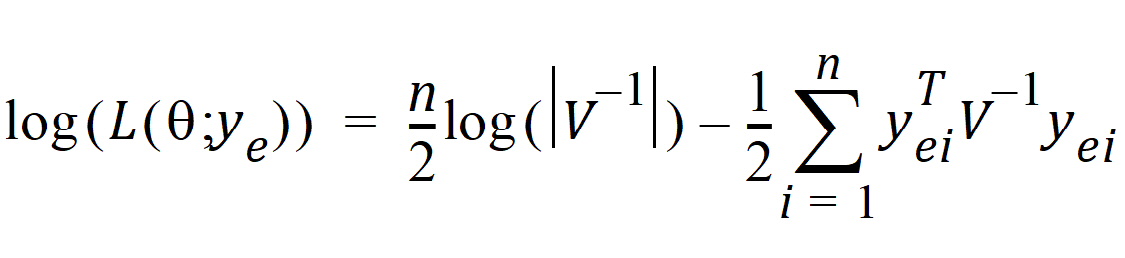
where V is the dispersion matrix for the multivariate normal distribution.
For more information on REML, see Corbeil and Searle (1976).