Average bioequivalence study designs
The most common designs for bioequivalence studies are replicated crossover, nonreplicated crossover, and parallel. In a parallel design, each subject receives only one formulation in randomized fashion, whereas in a crossover design each subject receives different formulations in different time periods. Crossover designs are further broken down into replicated and nonreplicated designs. In nonreplicated designs, subjects receive only one dose of the test formulation and only one dose of the reference formulation. Replicated designs involve multiple doses. A bioequivalence study should use a crossover design unless a parallel or other design can be demonstrated to be more appropriate for valid scientific reasons. Replicated crossover designs should be used for individual bioequivalence studies, and can be used for average or population bioequivalence analysis.
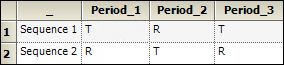
An example of a nonreplicated crossover design is the standard 2x2 crossover design described below.
Information about the following topics is available:
Recommended models for average bioequivalence
Power of the two one-sided t-tests procedure
Recommended models for average bioequivalence
The default fixed effects, random effects, and repeated models for average bioequivalence studies depends on the type of study design: replicated crossover, nonreplicated crossover, or parallel.
Replicated data is defined as data for which, for each formulation, there exists at least one subject with more than one observation of that formulation. The default models depend on the type of analyses and the main mappings. For replicated crossover designs, the default model used in the Bioequivalence object is as follows:
Fixed effects model: Sequence + Formulation + Period
Random effects model: Subject(Sequence) and Type: Variance Components
Repeated specification: Period
Variance Blocking Variables: Subject
Group: Treatment
Type: Variance Components
Nonreplicated crossover designs
Nonreplicated data is defined as data for which there exists at least one formulation where every subject has only one observation of that formulation. The default models depend on the type of analyses, the main mappings, and a preference called Default for 2x2 crossover set to all fixed effects (set under Edit > Preferences > LinMixBioequivalence). For nonreplicated crossover designs, the default model is as follows.
Fixed effects model: Sequence + Formulation + Period
Unless the bioequivalence preference Default for 2x2 crossover set to all fixed effects is turned on in the Preferences dialog (Edit > Preferences > LinMixBioequivalence), in which case the model is Sequence + Subject(Sequence) + Formulation + Period.
Random effects model: Subject(Sequence) and Type: Variance Components
Unless the bioequivalence preference Default for 2x2 crossover set to all fixed effects is turned on, in which case the model is not specified (the field is empty).
Repeated model is not specified.
Since there is no repeated specification, the default error model e ~ N(0, s2 I) is used. This is equivalent to the classical analysis method but using maximum likelihood instead of method of moments to estimate inter-subject variance. Using Subject as a random effect this way, the correct standard errors will be computed for sequence means and tests of sequence effects. Using a fixed effect model, one must construct pseudo-F tests by hand to accomplish the same task.
Note: If Warning 11094 occurs, “Negative final variance component. Consider omitting this VC structure.”, when Subject(Sequence) is used as a random effect, this most likely indicates that the within-subject variance (residual) is greater than the between-subject variance, and a more appropriate model would be to move Subject(Sequence) from the random effects to the fixed effects model, i.e., Sequence+Subject(Sequence)+Formulation + Period.
When this default model is used for a standard 2x2 crossover design, Phoenix creates two additional worksheets in the output called Sequential SS and Partial SS, which contain the degrees of freedom (DF), Sum of Squares (SS), Mean Squares (MS), F-statistic and p-value, for each of the model terms. These tables are also included in the text output. Note that the F-statistic and p-value for the Sequence term are using the correct error term since Subject(Sequence) is a random effect.
If the default model is used for 2x2 and the data is not transformed, the intrasubject CV parameter is added to the Final Variance Parameters worksheet:
intrasubject CV=sqrt(Var(Residual))/RefLSM
where RefLSM is the Least Squares Mean of the reference treatment.
If the default model is used for 2x2 and the data is either ln-transformed or log10-transformed, the intrasubject CV and intrasubject CV parameters are added to the Final Variance Parameters worksheet:
For ln-transformed data:
intersubject CV=sqrt(exp(Var(Sequence*Subject)) – 1)
intrasubject CV=sqrt(exp(Var(Residual)) – 1)
For log10-transformed data:
intersubject CV=sqrt(10^(ln(10)*Var(Sequence*Subject)) – 1)
intrasubject CV=sqrt(10^(ln(10)*Var(Residual)) – 1)
Note that for this default model Var(Sequence*Subject) is the intersubject (between subject) variance, and Residual is the intrasubject (within subject) variance.
For parallel designs, whether data is replicated or nonreplicated, the default model is as follows.
Fixed effects model: Formulation
There is no random model and no repeated specification, so the residual error term is included in the model.
Note: In each case, the model can be supplemented or modified to suit the analysis needs of the dataset. For example, if a Subject effect is appropriate for the Parallel option, as in a paired design (each subject receives the same formulation initially and then the other formulation after a washout period), set the Fixed Effects model to Subject+Formulation.
When mapping a new input dataset to a Bioequivalence object, if the mappings are identical for the new mapped dataset, then the model will remain the same. If there are any mapping changes other than mapping an additional dependent variable, then the model will be rebuilt to the default model since the existing model will not be valid anymore. This occurs for mapping changes either made manually or automatically (due to different column names in the dataset matching the mapping context).
Reset to the default model at any time by making any mapping change, such as unmapping and remapping a column.