-
Select the Method of computing the standard errors from the pulldown.
-
In the Confidence Level field, enter the confidence interval percentage.
-
From the Finite Difference Method pulldown, select the method for computing standard errors.
-
In the Step Size field, enter the standard error numerical differentiation step size. This is the relative step size to use for computing numerical second derivatives of the overall log likelihood function for model parameters when computing standard errors. This value affects all Run methods except IT2S-EM, which does not compute standard errors.
Auto-detect: When selected, NLME automatically chooses the standard error calculation method. Specifically, if both Hessian and Fisher score methods are successful, then it uses the Sandwich method. Otherwise, it uses either the Hessian method or the Fisher score method, depending on which method is successful. The user can check the Core Status text output to see which method is used.
Sandwich: The sandwich method has both advantages and disadvantages relative to the Hessian method. The main advantage is that, in simple cases, the sandwich method is robust for covariance model misspecification, but not for mean model misspecification. The main disadvantage is that it can be less efficient than the simpler Hessian-based method when the model is correctly specified.
Hessian: The Hessian method of parameter uncertainty estimation evaluates the uncertainty matrix as R-1, where R-1 is the inverse of the second derivative matrix of the -2*Log Likelihood function.
Standard errors for the parameter estimators for individual models are computed using the Hessian method. The Hessian method evaluates the uncertainty matrix as R-1, where R-1 is the inverse of the second derivative matrix of the -2*Log Likelihood function.
Fisher Score: The Fisher Score method is fast and robust, but less precise than the Sandwich and Hessian methods.
None: No standard error calculations are performed.
Central Difference: The second-order derivative of f uses the form:
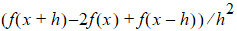
Forward Difference: The second-order derivative of f uses the form:
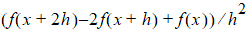
Note:Computing the standard errors for a model can be done as a separate step after model fitting. This allows the user to review the results of the model fitting before spending the time computing standard errors.
For engines other than QRPEM:
– After doing a model fitting, accept all of the final estimates of the fitting.
– Set the number of iterations to zero.
– Rerun with a method selected for the Finite Difference Method option.
For QRPEM, use the same steps, but also request around 15 burn-in iterations.
