THETA Transformation
THETA Parameter Relative Standard Error (RSE) Calculation
OMEGA Transformation
SIGMA Transformation
It is sometimes preferable to write non-linear mixed effects models with parameters in the log domain to ensure that they remain positive or to stabilize their variance. A common use case is “mu-referencing”, e.g., the expression for CL
CL = THETA(1) * EXP(ETA(1))
can be written as
MU_1 = LOG(THETA(1))
CL = EXP(MU_1+ETA(1))
In the above example, MU_1 is the natural log of the typical value of CL. Pirana allows display of this LOG(CL) value (default), or the exp(THETA) box can be checked to back-transform the estimate to original scale.
THETA Parameter Relative Standard Error (RSE) Calculation
Percent Relative Standard Error for THETA parameters are calculated as:
RSE(%) = (SE / Estimate) * 100
where:
SE is the standard error of the estimated parameter (THETA)
Estimate is the estimated value of the parameter (THETA)
The RSE provides a measure of the precision or relative uncertainty associated with the estimated parameter. A smaller RSE indicates a more precise estimate with less uncertainty, while a larger RSE indicates a less precise estimate with higher uncertainty. It is important to note that the calculation of the RSE assumes that the standard errors and estimates follow a normal distribution and that the estimated parameter is not near zero or negative. Additionally, the RSE should be interpreted in the context of the specific parameter being estimated and the modeling assumptions and objectives of the analysis.
Note: RSE calculation depends on a successful covariance step. RSE will not be reported if SEs are not available.
The calculation options for transforming the variances include: Untransformed. sqrt(OM^2), and sqrt(exp(OM^2) – 1.
Untransformed
OMEGA matrix diagonal elements = Estimate(%RSE)
where:
Estimate is the diagonal element of the OMEGA matrix as reported by the estimation engine
%RSE is calculated as described below
Percent Relative Standard Error (RSE(%)) = (SE / Estimate) * 100
where:
SE is the standard error of the estimated parameter (OMEGA diagonal element)
Estimate is the estimated value of the parameter (OMEGA diagonal element)
OMEGA matrix off-diagonal elements = Estimate(SE)
where:
Estimate is the off-diagonal element of the OMEGA matrix as reported by the estimation engine
SE is the standard error of the off-diagonal element of the OMEGA matrix as reported
sqrt(OM^2)
OMEGA matrix diagonal elements = 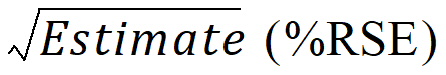
where:
Estimate is the diagonal element of the OMEGA matrix as reported by the estimation engine
%RSE is calculated as described below
OMEGA diagonal elements are variances. Taking the square root produces a standard deviation. For log normal distributions, standard deviation approximates %CV, which is a generally understood measure of variability, and is often preferred when communicating analysis results. This approximation loses accuracy as the magnitude of OMEGA estimate increases. For large OMEGA estimates, the alternative transformation described in the next section is preferred.
Percent Relative Standard Error = %RSEuntransformed/2
OMEGA matrix off-diagonal elements = correlation(SE)
where:
correlation = Correlation of OMEGA matrix off-diagonal element as reported in the OMEGA matrix correlation sub-matrix by the estimation engine
SE = Standard error of the off-diagonal element of the OMEGA matrix as reported
The correlation matrix provides insights into the relationships between different random effects parameters. The correlation matrix helps identify parameters that are highly correlated. Strong correlations between parameters can affect model estimation and may indicate redundancies or collinearity in the model. Identifying such correlations can guide model refinement and potentially lead to parameter simplification or re-parameterization.
sqrt(exp(OM^2) – 1)
Note: This transformation is appropriate for log-normal structural parameter forms such as CL = TVCL * exp(ETA(1)). In this case, the transformation will give a closer approximation to the true CV than the sqrt(OM^2) transformation.
OMEGA matrix diagonal elements = 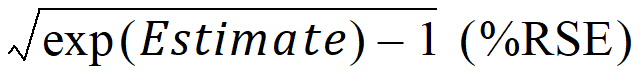
where:
Estimate is the diagonal element of the OMEGA matrix as reported by the estimation engine
%RSE is calculated as described below
Percent Relative Standard Error = exp(Estimate) / (2 * (exp(Estimate) – 1)) * Estimate * (%RSEuntransformed)
OMEGA matrix off-diagonals = correlation(SE) as described above.
SIGMA transformations are the same as used for OMEGA.
Untransformed
SIGMA diagonals %RSE = (SE / Estimate) * 100
where:
– SE is the standard error of the estimated parameter (SIGMA diagonal element)
– Estimate is the estimated value of the parameter (SIGMA diagonal element)
SIGMA off-diagonal elements are reported as Estimate(SE)
sqrt(OM^2)
SIGMA diagonals = 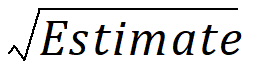
SIGMA diagonal %RSE = (%RSEuntransformed)/2
SIGMA off-diagonals are reported as correlation(SE)
sqrt(exp(OM^2) – 1)
SIGMA diagonals = 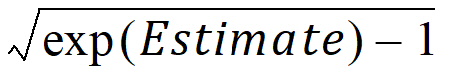
SIGMA diagonal %RSE =
exp(Estimate) / (2 * (exp(Estimate) – 1)) * Estimate * (%RSEuntransformed)
SIGMA off-diagonals are reported as correlation(SE)