The calculation options for transforming the variances include:
Untransformed
sqrt(OM^2)
sqrt(exp(OM^2) – 1
When Untransformed is selected:
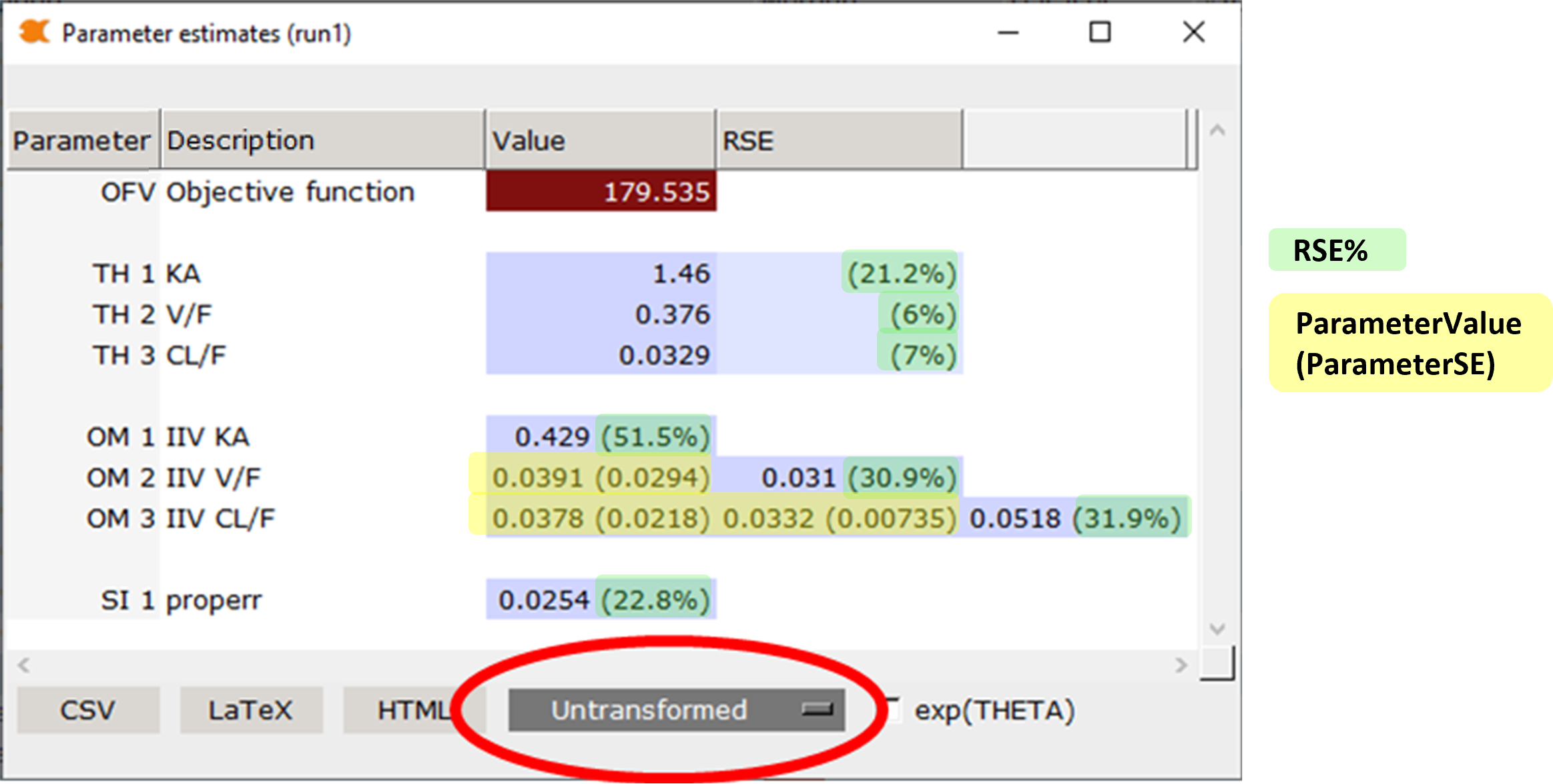
OMEGA matrix diagonal elements are reported as:
Estimate(%RSE)
where:
Estimate is the diagonal element of the OMEGA matrix as reported by the estimation engine
%RSE is calculated as described below
Percent Relative Standard Error for OMEGA diagonal elements are calculated as:
RSE(%) = (SE / Estimate) * 100
where:
SE is the standard error of the estimated parameter (OMEGA diagonal element)
Estimate is the estimated value of the parameter (OMEGA diagonal element)
OMEGA matrix off-diagonal elements are reported as:
Estimate(SE)
where:
Estimate is the off-diagonal element of the OMEGA matrix as reported by the estimation engine
SE is the standard error of the off-diagonal element of the OMEGA matrix as reported
When sqrt(OM^2) is selected:
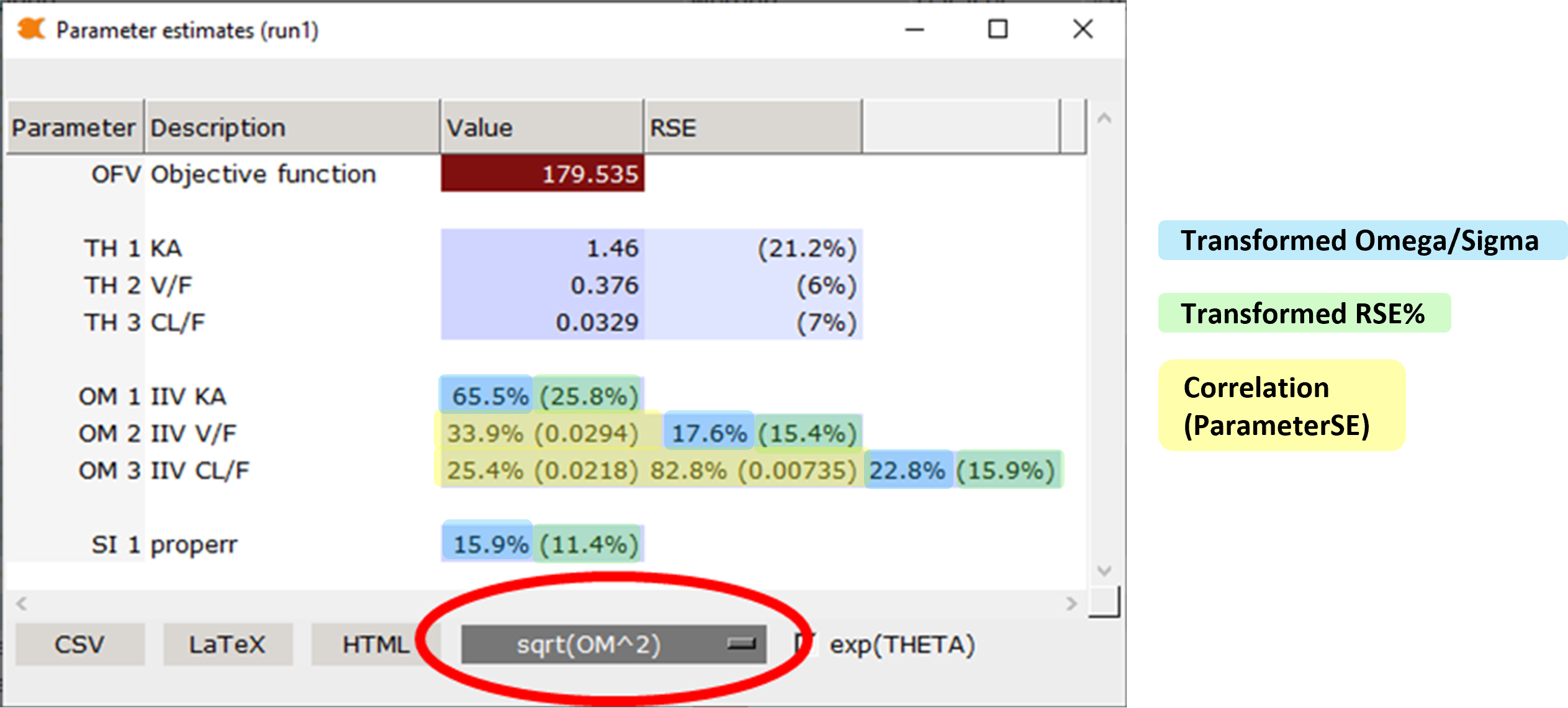
OMEGA matrix diagonal elements are reported as:
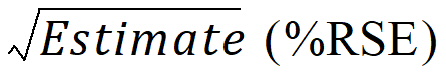
where:
Estimate is the diagonal element of the OMEGA matrix as reported by the estimation engine
%RSE is calculated as described below
OMEGA diagonal elements are variances. Taking the square root produces a standard deviation. For log normal distributions, standard deviation approximates %CV, which is a generally understood measure of variability, and is often preferred when communicating analysis results. This approximation loses accuracy as the magnitude of OMEGA estimate increases. For large OMEGA estimates, the alternative transformation described in the next section is preferred.
Percent Relative Standard Error for OMEGA diagonal elements are calculated as:
%RSEuntransformed/2
OMEGA matrix off-diagonal elements are reported as:
correlation(SE)
where:
correlation is the correlation of the off-diagonal element of the OMEGA matrix as reported in the correlation sub-matrix of the OMEGA matrix by the estimation engine
SE is the standard error of the off-diagonal element of the OMEGA matrix as reported
The correlation matrix provides insights into the relationships between different random effects parameters. The correlation matrix helps identify parameters that are highly correlated. Strong correlations between parameters can affect model estimation and may indicate redundancies or collinearity in the model. Identifying such correlations can guide model refinement and potentially lead to parameter simplification or re-parameterization.
When sqrt(exp(OM^2) – 1) is selected:
Note: This transformation is appropriate for log-normal structural parameter forms such as CL = TVCL * exp(ETA(1)). In this case, the transformation will give a closer approximation to the true CV than the sqrt(OM^2) transformation.
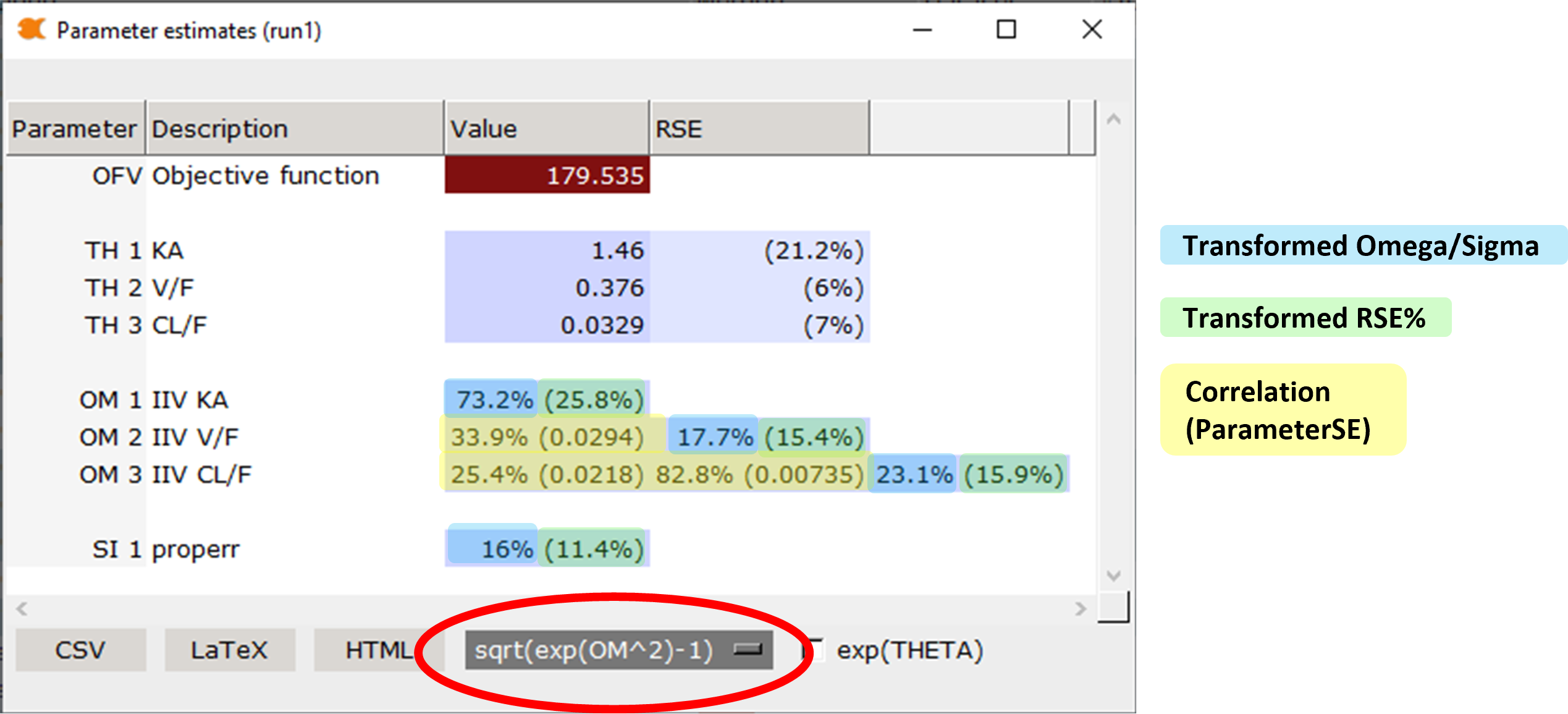
OMEGA matrix diagonal elements are reported as:
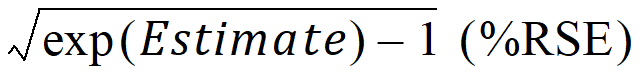
where:
Estimate is the diagonal element of the OMEGA matrix as reported by the estimation engine
%RSE is calculated as described below
OMEGA diagonal %RSE is calculated as:
exp(Estimate) / (2 * (exp(Estimate) – 1)) * Estimate * (%RSEuntransformed)
OMEGA matrix off-diagonals are reported as correlation(SE) as described above.