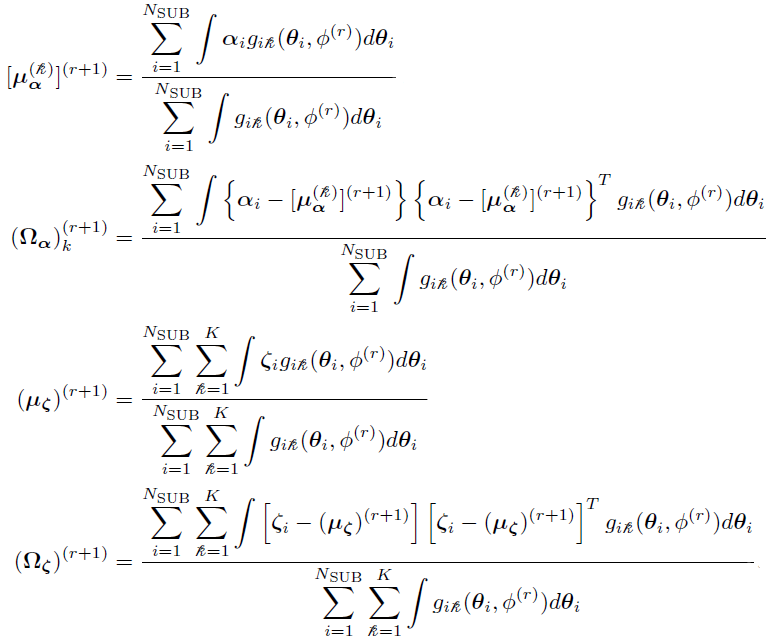In the EM algorithm, both complete data and missing data are defined:
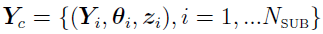defines the complete data.
{
,
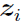} is missing data, where is a K-dimensional vector whose 
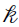th component, 
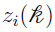, is 1 or 0 depending on whether 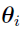belongs to the 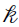th mixing in the equation:
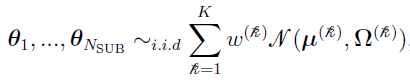
where
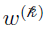is the weight for the 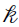th Gaussian distribution 
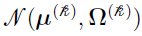(nonnegative number, normalized by 
)
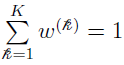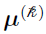is the mean vector (
)
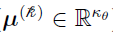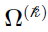is the positive definite covariance matrix (
)
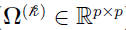The purpose of the EM algorithm is to start with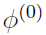 
and iterate from 
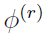to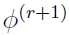 
at the rth iteration, continuing the process until the desired parameters 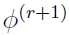are identified, such that
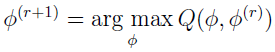
where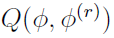 
is defined and calculated by equations discussed below. This process guarantees convergence to a stationary point of the likelihood [3] [11] [12], and typically, a number of starting positions are suggested in an effort to ensure convergence to a global maximum [3].
The E-Step
During the Expectation Step, the function is defined as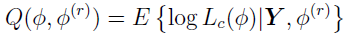 
, where the complete data likelihood 
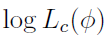is given by
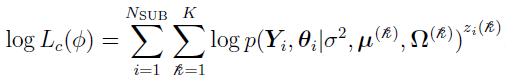
By using Bayes Theorem, the function can be written as [3]
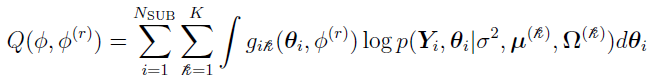
where
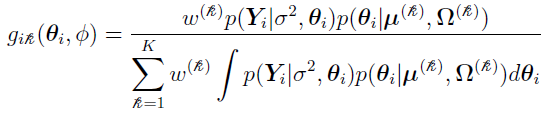
and, for some constant C,
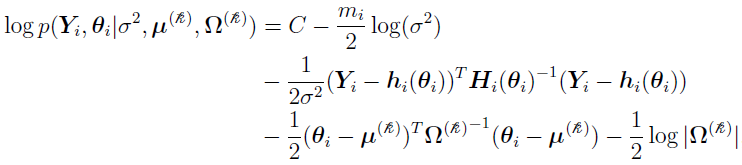
Note that the probability that the ith individual belongs to the 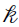th mixing component can be defined as
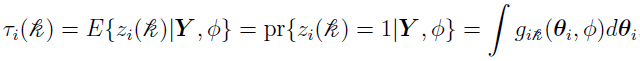
The M-Step
In the Maximization Step, it is sufficient to find the unique solution of 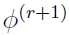such that
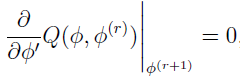
where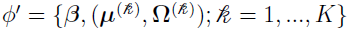 
. This leads to unique solutions [3] of 
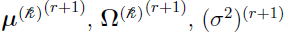. (See the “Solutions” section for details.)
The updating of 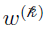can be calculated as the average of the contributions from each subject to the 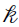th mixing [3], i.e.,
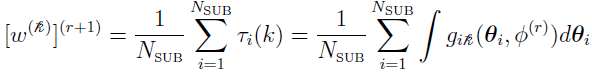
To calculate the log of the likelihood functio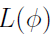n 
in
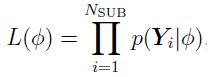
(discussed in “Two-Stage Nonlinear Random Effects Mixture Model”) first evaluate the denominator of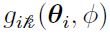 
, which does not depend on 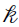. Define it as Ni such that
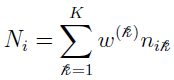
where
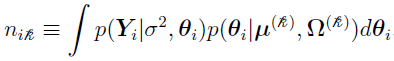
Once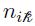 
and Ni are obtained, the earlier equation:
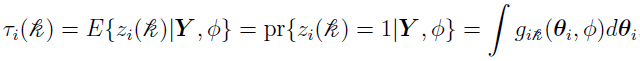
can be immediately evaluated by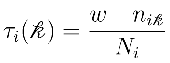 
The log of the likelihood function 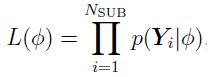is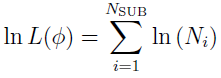 
.
The EM iterates 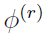have the important property that the corresponding likelihoods 
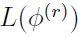are non-decreasing, i.e., 
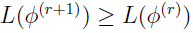for all r [11] [3].
Looking at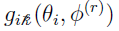 
(from the E-step)
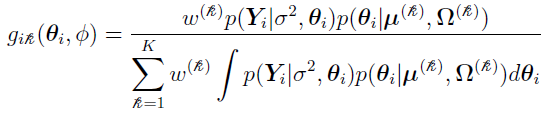
leads to the conclusions that
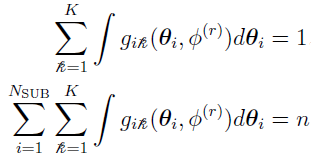
Therefore, the unique solutions [3] of 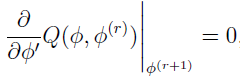(from the M-step) can be written as
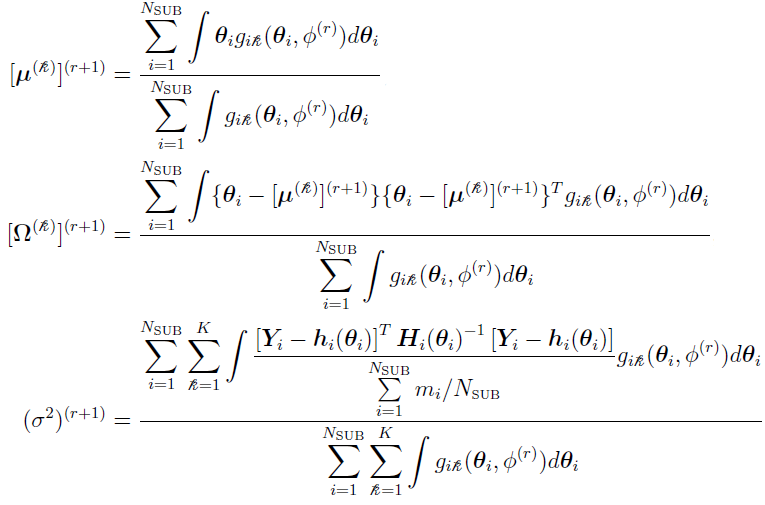
In a case described in reference [3], the parameter 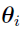can be partitioned into two components 
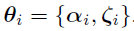, where
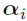is from a mixture of multivariate Gaussians.
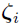is from one single multivariate Gaussian.
The EM updates from 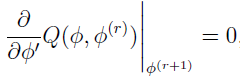are given by
