The Michaelis-Menten models describe the relationship between the rate of substrate conversion by an enzyme to the concentration of the substrate. These kinetics are valid only when the concentration of substrate is higher than the concentration of enzyme, and in the case of steady-state, where the concentration of the complex enzyme-substrate is constant.
The Phoenix library contains four Michaelis-Menten models that use constants to supply the dosing information. The required number of constants are listed below under each model number. For an explanation of dosing constants see the “Dosing constants for Michaelis-Menten models” section.
Phoenix assumes that the time of the first dose is zero. For these models, times in the dataset must correspond to the dosing times, even if these times contain no observations. In this case, include a column for Weight in the dataset, and weight the observations as zero.
These models parameterize Vmax in terms of concentration per unit of time.
For a discussion of the difficulties in fitting the Michaelis-Menten models, see:
Tong and Metzler (1980). Mathematical properties of compartment models with Michaelis-Menten-type elimination. Mathematical Biosciences 48:293–306.
Metzler and Tong (1981). Computational problems of compartmental models with Michaelis-Menten-type elimination. J Pharmaceutical Sciences 70:733–7.
Model 301
One-compartment with bolus input and Michaelis-Menten output.
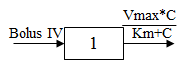
C(t) is the solution to the differential equation:
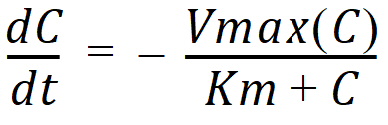
with initial condition C(0)=D/V.
Required constants: Number of doses (N), Dose amount for dose N, Time of dose for dose N
Estimated parameters: V is the volume, Vmax is the max elimination rate, Km is the Michaelis constant
Secondary parameters: AUC=(D/V)(D/V/2+Km)/ Vmax
Model 302
One-compartment with constant IV input and Michaelis-Menten output (1cp MM infus).
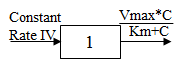
C(t) is the solution to the differential equations:
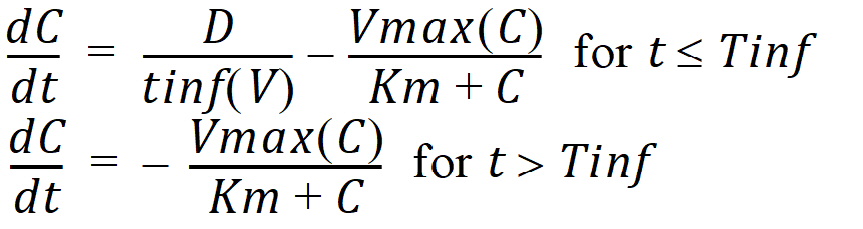
with initial condition C(0)=0.
Required constants: Number of doses (N), Dose amount for dose N, Start time of dose for dose N, End time for dose N
Estimated parameters: V is the volume, Vmax is the max elimination rate, Km is the Michaelis constant
Secondary parameters: None
Model 303
One-compartment with first-order input, Michaelis-Menten output and no lag time (1cp MM xvas).
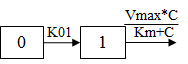
C(t) is the solution to the differential equation:
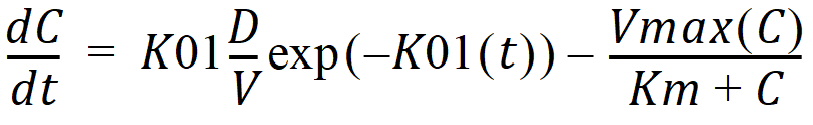
with initial condition C(0)=0.
Required constants: Number of doses (N), Dose amount for dose N, Time of dose for dose N
Estimated parameters: V_F, K01 is the absorption rate, Vmax is the max elimination rate, Km is the Michaelis constant
Secondary parameters: K01 half-life
Model 304
One-compartment with first-order input, Michaelis-Menten output and lag time (1cp MM xvas lag).
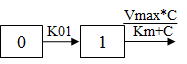
C(t) is the solution to the differential equation:
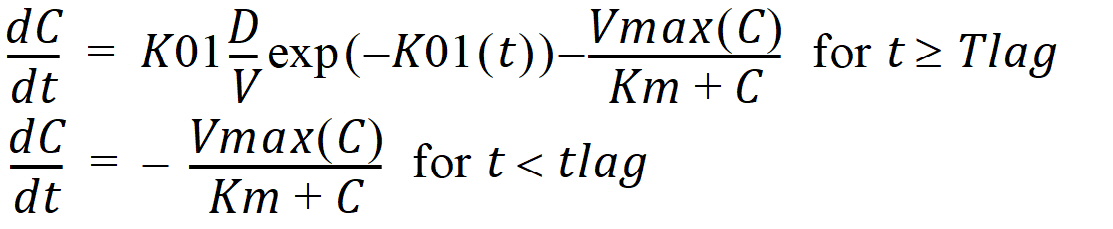
with initial condition C(0)=0.
Required constants: Number of doses (N), Dose amount for dose N, Time of dose for dose N
Estimated parameters: V_F, K01 is the absorption rate, Vmax is the max elimination rate, Km is the Michaelis constant, Tlag is the lag time
Secondary parameters: K01 half-life