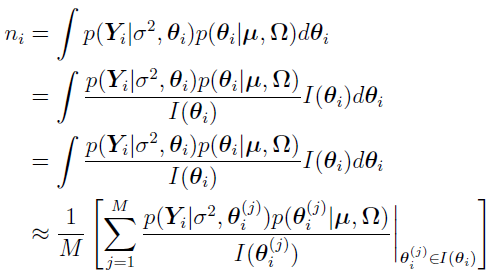How QRPEM Calculates Population Parameters
The current QRPEM code, as of 2023, does not include a mixture model, so the number of mixture K is set to 1. However, the mixture label K can be removed. For example,
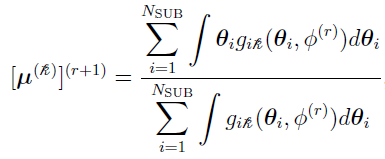
(discussed in “Solutions”) can be written as
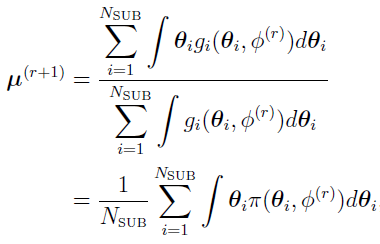
where
is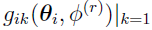 
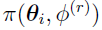is the joint likelihood:
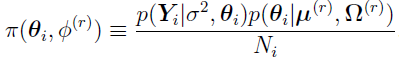
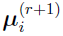can be defined as the (r +1)th iteration’s Bayes estimates of the mean for subject i,
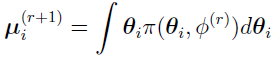
and the initial equation becomes
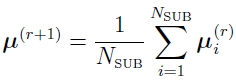
In fact, this equation is Eq.(8) in reference [17], and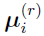 
replaces xi.
Similarly,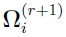 
can be defined as the (r+1)th iteration’s Bayes estimates of the covariance for subject i,
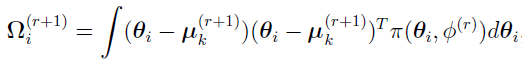
and the equation:
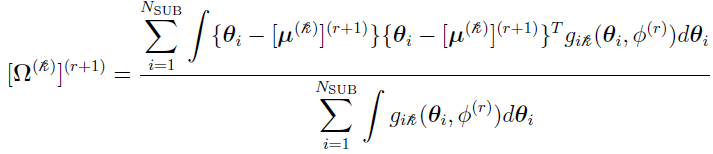
(discussed earlier) for K = 1 become
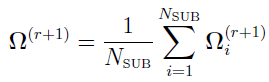
All the calculations which involve the integral over are performed using the Monte Carlo method with an importance sampling function I(
). In the current NLME engine, by default I(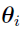) is a multivariate normal distribution, whose mean and covariance are 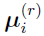and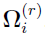 
, respectively. (Note that the NLME engine also provides direct sampling, double exponential, multivariate t, mixture-2, and mixture-3. In addition, for the multivariate normal distribution case, the mean and covariance used depends on whether MAP assistance is enabled or not.)
Take the calculation of 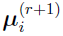as the importance sampling function, for example.
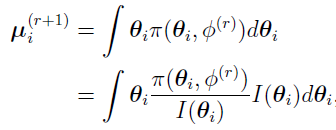
In principle, the role of I(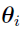) is to mimic the shape of 
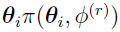, so that the variance of the Monte Carlo estimator of 
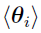is kept as low as possible [18] [2]. To calculate 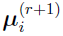, its biased estimator [18] [2] 
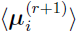is used. The weight 
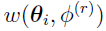is defined as
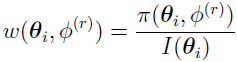
Then
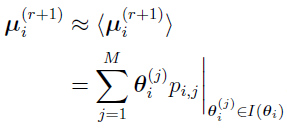
where
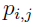is a normalized weight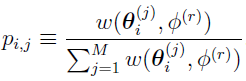 
(the same as the 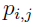in Eq.(3) in reference [17], normalized by 
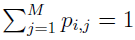and ).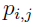
M is the total number of samples (in QRPEM, usually M = 300).
(j) in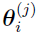 
means the jth sample of .
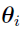All the 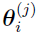are sampled from the importance sampling function I().
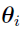Notes:
When using the biased estimator equation, the normalization factor of I(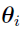) does not matter, since it will be canceled in the numerator and the denominator in this equation.
QRPEM does not just ‘randomly’ sample from the importance sampling function I(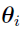). Instead, the samples of 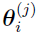are ‘quasi-randomly’ sampled by using the so called low discrepancy quasi-random sequence. In particular, QRPEM uses a Sobol sequence. The advantage of using quasi-random samples is that, for purposes of numerical integration, sampling from the parameter space of I(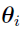) is done much more evenly than purely random sampling. As a result, QRPEM usually provides far more accurate integral values for a given sample size. In other words, QRPEM typically gives accurate results using a much smaller Monte Carlo sample size than other MCPEM methods. Therefore, QRPEM is usually much faster than other MCPEM methods, without compromising accuracy.
For the total log likelihood, since there is no Gaussian mixture, ln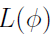
is
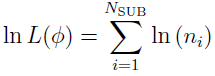
where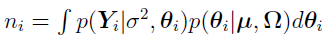 
. The same M quasi-random samples of 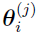sampled from the importance sampling function I(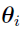) using the low-discrepancy Sobol sequences, can be used to evaluate ni as follows,
