How QRPEM Calculates Covariate Parameters
Linear regression is used to find the covariate parameters such as dCldWt, etc.
In this equation:
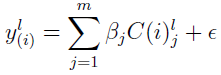
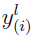is the lth element in the averaged structural parameter array for subject i.
C(i)lj is the (l, j) element in the C matrix for subject i.
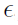is the noise term.
Looking at the matrix form in the “C Matrix example” section,
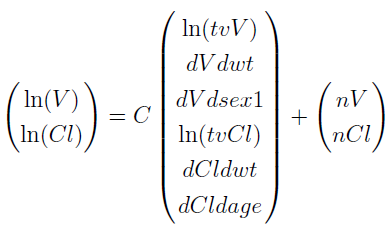
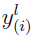is the lth element in the vector 
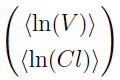for subject i.
where
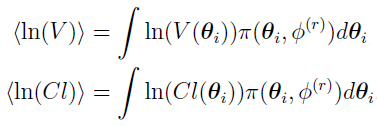
Both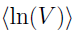 
and 
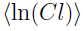are obtained by averaging the samples of ln(V(
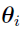)) and ln(Cl(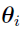)) during the Monte Carlo process.
The C(i)lj in the first equation of this section
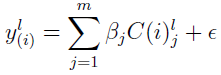
is the element in the lth row and jth column of the C matrix for subject i. In this example, the C matrix is the 2 by 6 matrix as shown below
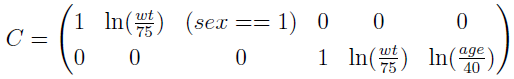
Each subject has a different C matrix. The size of the C matrix is leneta (number of unfrozen etas) by nbasetheta (number of unfrozen population (typical) parameters plus the covariate parameters.
The 
j in the first equation of this section is the jth element of the vector to be obtained by linear regression.
In this example, the vector is
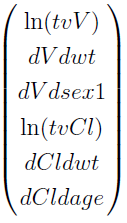
and is the same across all the subjects.
To find , first sum over all the subjects, i.e.,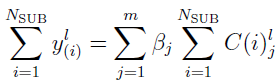 
.
Defining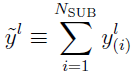 
and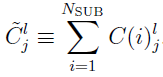 
, and taking 
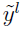as the lth element in the 
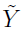vector,
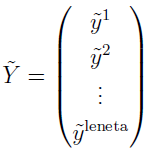
and taking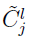 
as the (l, j) element of the 
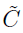matrix, i.e.,
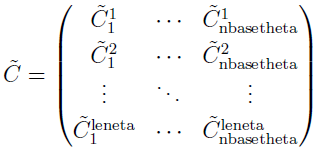
Then the earlier summation:
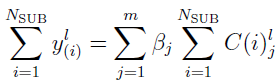
can be written as the matrix form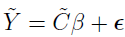 
, where 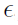is a noise vector. The purpose of the linear regression is to find the vector such that the noise ϵ is minimized. The least-squares estimation of is by simply solving the for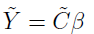 
.
can be found by calling the LAPACK subroutine DPOTRF followed by DPOTRS. In fact, in QRPEM, it is trying to find a from the equation 
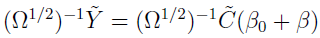, where 0 is the from the last iteration, and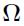 
is just the covariance matrix of the population parameters.
Defining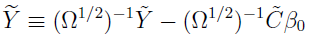 
and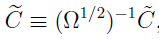 
, the previous equation becomes .
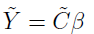Again, is found by calling the LAPACK subroutine DPOTRF followed by DPOTRS. The new for the next iteration is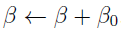 
.