Convergence Criteria for QRPEM
Four convergence options are provided for QRPEM.
Default: Check convergence for both log-likelihood and population parameters theta and sigma.
-2LL and all params: Check convergence for both log-likelihood and all population parameters (theta, sigma, and Omega).
-2LL only: Check convergence for log-likelihood only.
All params only: Check convergence for all population parameters (theta, sigma, and Omega) only.
The stopping criterion for log-likelihood and/or population parameters across all options is based on the linear regression test, except for log-likelihood in the Default option, where it compares the averages of the current 10 iterations with the previous 10 iterations.
Stopping Criteria for the Log-Likelihood in the Default option
The stopping criteria of the log-likelihood, lnL, in the Default option, can be described as follows.
After every 10 iterations, calculate the average lnL for that set of 10 iterations.
Compare the average lnL for the latest iteration set with that for the previous set.
If lnL for the latest iteration set is less than or equal to the lnL for the previous set, the latest iteration is marked as converged.
If not, 10 more iterations are completed and the comparison of lnLs is repeated.
Note: Mathematically, the lnL for the latest iteration set will never be smaller than the lnL for the previous set. However, QRPEM uses the Monte Carlo method to numerically estimate the lnL at each of the iterations, so there is uncertainty. Therefore, numerically, it is entirely possible.
Stopping Criteria based on the linear regression test
QRPEM stores the values of each population parameter (or log-likelihood) from the latest n iterations. Let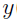 
denote the array of stored values of the population parameter (or log-likelihood) with its ith element as 
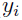, where i = 1, 2,..., n. The relationship between 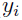and i is modeled by:
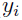
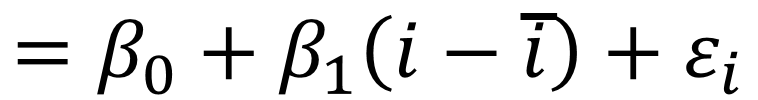, i = 1, 2,...,n
where parameters 
0 and 1 represent the intercept and slope,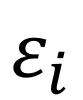 
denotes the error, and i = (n+1)/2.
To determine if the elements 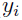are flattened, test whether the null hypothesis can be rejected.
Null hypothesis:
Alternative hypothesis:
To do this, calculate the t statistic [19] [20]
t-statistic =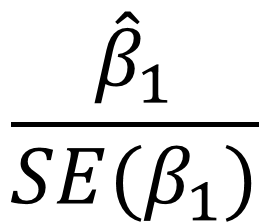 
Here,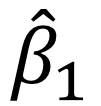 
denotes the estimate for the slope 1 and SE(1) is the standard error of 1
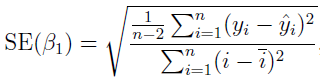
where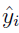 
is the predicted parameter value at i, using the 0 and the slope 1 obtained from the linear regression.
If the absolute value of t-statistic is less than or equal to the critical value, then it concludes that 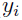is flattened and its associated population parameter (log-likelihood), whose latest 10 iterations are stored in 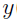, is converged. For the population parameter, once it is determined as converged, QRPEM will not check its convergence again.
Note: For the Default option, the convergence test starts at iteration 40 and is then performed every 10 iterations, whereas, for the remaining options, it starts at iteration (n+1) and is then performed at every iteration.