Four hypotheses are of interest:
no sequence effect (or drug residual effect);
no treatment effect given no sequence effect;
no period effect given no sequence effect; and
no treatment and no sequence effect.
Hypothesis 1 above can be tested using the Wilcoxon statistic on the sum S. If R(Sl) is the rank of Sij in the whole sample, l = 1,…, n+m. The test statistic is:
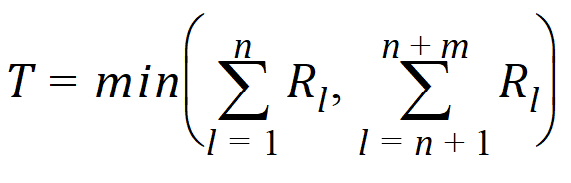
The p-value is evaluated by using normal approximation (Conover, 1980):
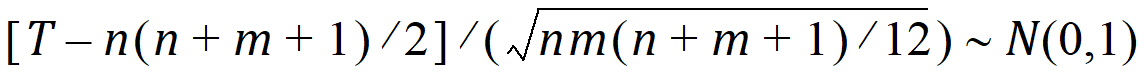
Similarly, hypothesis 2 can be tested using the Wilcoxon statistic on the difference D; hypothesis 3 can be tested using the Wilcoxon statistic on the crossover difference C. The statistics are in the form described above.
Hypothesis 4 can be tested using the bivariate Wilcoxon statistic on (Yij1, Yij2). For each period k, let Rijk equal:
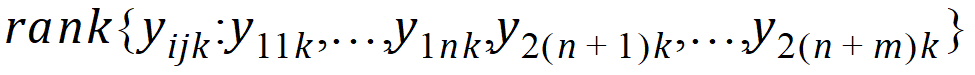
The average rank for each sequence is:
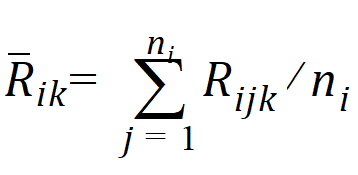
where j=1,…, ni, ni=n for i=1, and ni=m for i=2
Thus, the statistic to be used for testing hypothesis 4 is:
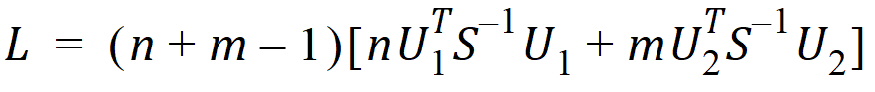
where Ui is a 2x1 vector: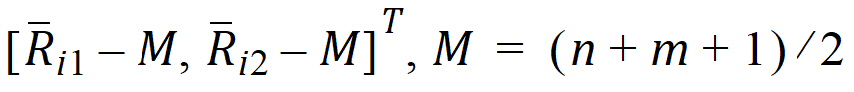
S is the 2x2 covariance matrix: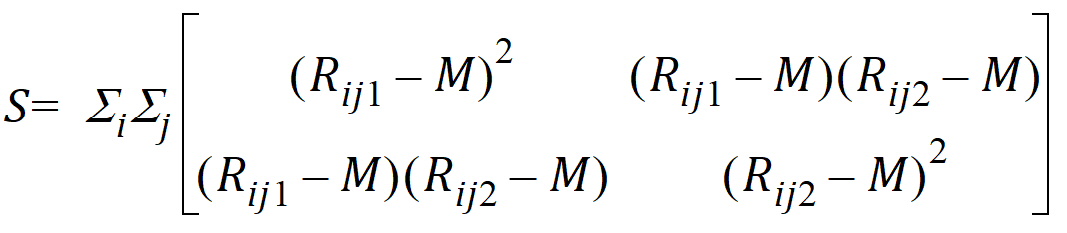
and L ~ X2, so the p-value can be evaluated.