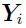— The observation vector for subject i. It is called the response vector [1].
— The jth observation for subject i in the data set. It is the jth element in the 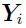vector.
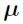— The mean vector for the population parameters. Also called a Fixed effect parameter, THETA, or theta.
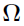— The covariance matrix of the multivariate Gaussian whose mean is 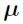. It is the inter-individual variance-covariance matrix. Also referred to as OMEGA or omega, which means the standard deviation of the Gaussian.
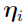— The random effect [25] [1] vector with mean 0 and variance-covariance matrix 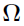(inter-individual variability). Also called ETA or eta.
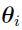— The population parameter vector in the model that accounts for the inter-individual variability. It is the parameter vector describing the unobserved random effects. It is the fixed effect 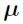plus the random effect 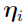, i.e., = +.
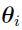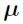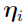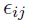— The residual error for subject i at the jth observation, which is an independent and identically (i.i.d.) normally distributed random variable with mean of zero and standard deviation 
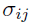(or variance 
).
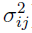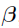— The unobserved fixed effect parameter vector that is common to all subjects (often referred to as bare fixed effects as they are not paired with any random effects) to observation . It can be the collection of covariate parameters.
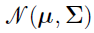— The multivariate Gaussian distribution with mean 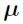and covariance matrix 
.
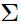NSUB — The number of subjects in the data set.
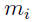— The number of observations for subject i in the data set.
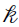— The 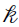th mixture in the Gaussian mixture model. For now, NLME does not support Gaussian mixture models, the 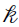can be removed or simply set as 1.
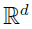— d-dimensional real space
T (superscript) — The transpose of a vector or a matrix.