Semicompartmental calculations
Phoenix’s semicompartmental modeling estimates effect-site concentrations for given times and plasma concentrations and an appropriate value of Ke0. This function should be used when a counterclockwise hysteresis is observed in the graph of effect versus plasma concentrations. The hysteresis loop collapses with the graph of effect versus effect-site concentrations.
A scientist developing a PK/PD link model based upon simple IV bolus data can use this function to compute effect site concentrations from observed plasma concentrations following more complicated administration regimen without first modeling the data, i.e., semicompartmental modeling determines if the hysteresis can be collapsed using an effect compartment, without requiring a full compartmental model. The results can then be compared to the original datasets to determine if the model suitably describes pharmacodynamic action after the more complicated regimen.
Drug concentration in plasma Cp for each subject is measured at multiple time points after the drug is administrated. To minimize the bias in estimating Ce, the time points need to be adequately sampled such that accurate estimation of the AUC by noncompartmental methods can be obtained. Effect-site link model is used and the value of the equilibration rate constant ke0 that accounts for the lag between the Cp and the Ce curves is required. The default option is for a piecewise Linear/Log model to be assumed for Cp.
In the effect-site link model proposed by Sheiner, Stanski, Vozeh, Miller and Ham (1979), a hypothetical effect compartment was proposed to model the time lag between the PK and PD responses. The effect site concentration Ce is related to Cp by first-order disposition kinetics and can be obtained by solving the differential equation:
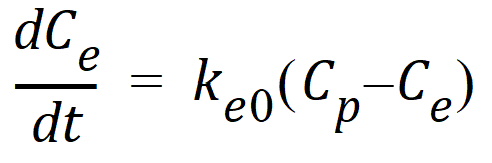
where ke0 is a known constant. In order to solve this equation, one needs to know Cp as a function of time, which is usually given by compartmental PK models.
Here, use a piecewise linear model for Cp:
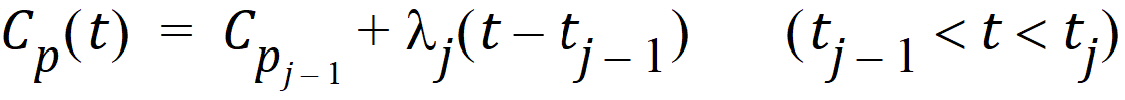
where:
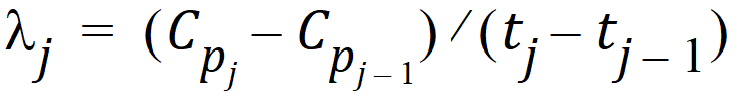
and:
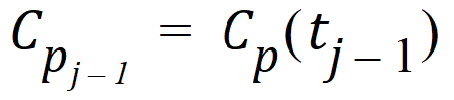
Using the above two equations can lead to a recursive equation for Ce:
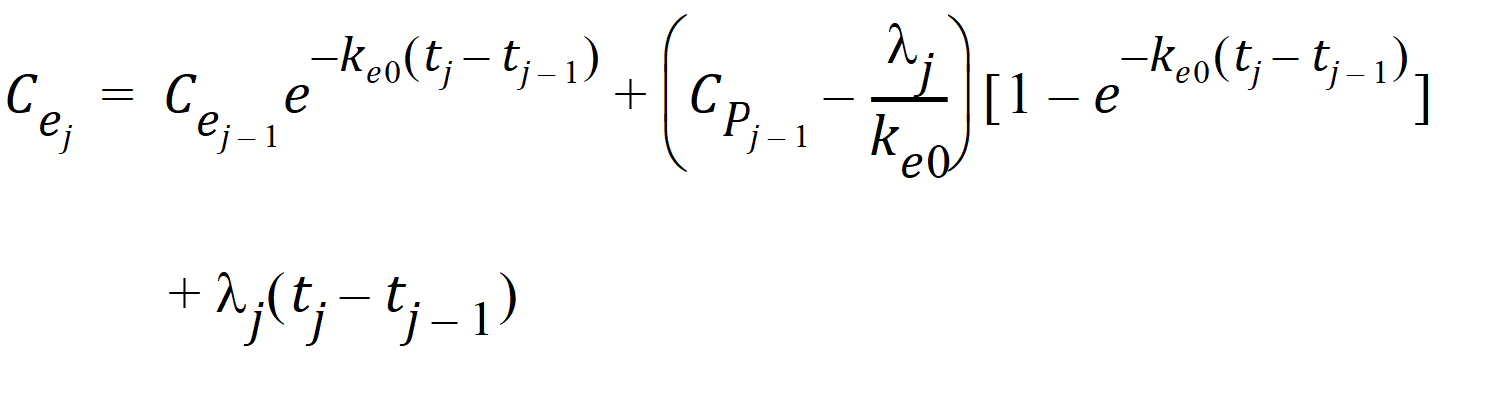
The initial condition is Cp(0)=Ce(0) =0.
One can also assume a log-linear piecewise PK model for Cp:
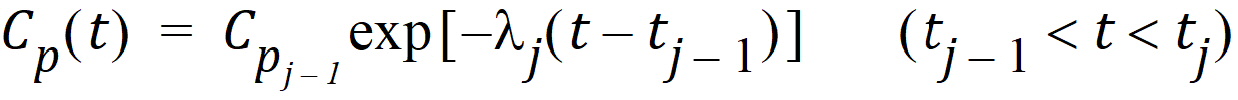
where:
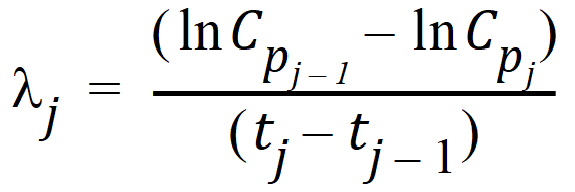
and:
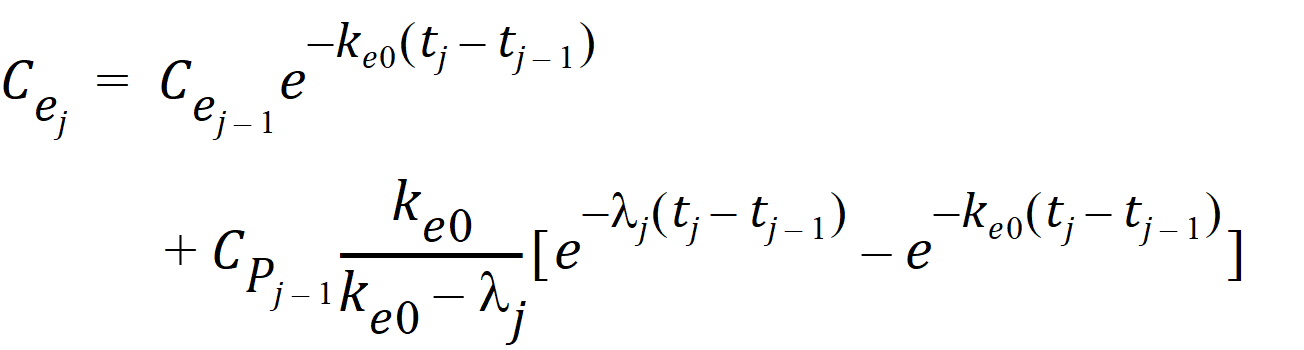
l1 and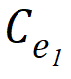 
are estimated by a linear regression, assuming Ce(0) = Cp(0) = 0.
Phoenix provides three methods. The ‘linear’ method uses linear piecewise PK model; the ‘log’ method uses log-linear piecewise PK model; the default ‘log/linear’ method uses linear to Tmax and then log-linear after Tmax. The Effect field is not used for the calculation of Ce but when it is provided, the E vs Cp and E vs Ce plots will be plotted.
Kowalski ad Karim (1995). A semicompartmental modeling approach for pharmacodynamic data assessment, J Pharmacokinet Biopharm 23:307–22.
Sheiner, Stanski, Vozeh, Miller and Ham (1979). Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharm Ther 25:358–71.