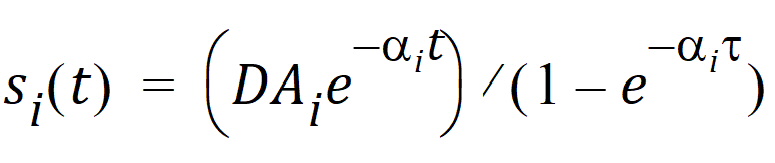Closed form computations for 1, 2, and 3-compartment first-order library models with simple single compartment dosing are handled recursively, where the model solution is defined by n residue parameters Ai which sum to one and exponential decay rates ai. These parameters are derived from micro constants in the usual way via Laplace transforms assuming unit dose (including convolution with an extra exponential for first-order input).
There is a “state vector” [s1(t),…,sn(t)] representing the model at any point in time, where each state component is a term in the overall solution corresponding to a particular decay rate ai. Each separate state evolves over time in the following way, where r is the infusion rate into a single predefined compartment:
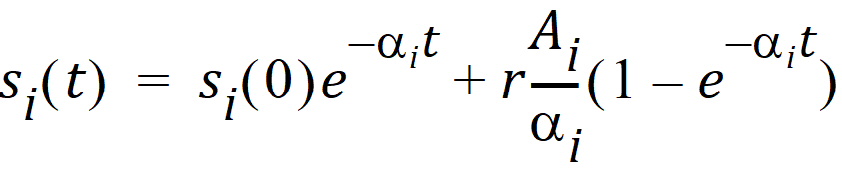
The output value of the model, which is usually an amount in a specified compartment, at a point in time is the sum of the state vector components:
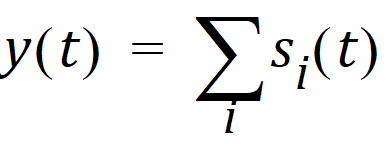
When a bolus dose D is administered, the state is modified in the following way:
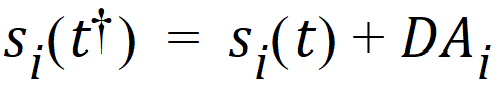
Regarding cfMicro models, the above description models the central compartment amount as a function of input to the depot compartment, whether central or absorption. However, the actual implementation must consider the following complicating factor.
Since, in general, models can depend on covariates that change discontinuously with time, the closed-form models must not only model the central compartment as a function of dosing to the depot, but they must also model every compartment as a function of every other compartment. The reason is that, if a covariate is changed, three steps must be performed:
Record the amount in every compartment.
Empty the system and calculate the new parameters of the model.
Put back the prior amounts into the compartments as if they were bolus doses, thus restoring all compartments to their prior amounts.
If the model allows dosing to both central and absorption compartments, this is done using the above scheme, since doses can go into both compartments.
In the steady-state case with bolus dose D given at intervals t, the solution takes the form: