This section provides example modeling code for the following cases.
Multinomial (ordered categorical)
Time to event model (exponential)
Emax (Hill) model with exponent
One-compartment IV bolus population PK
One-compartment IV bolus, two parallel models with common fixed effects
One-compartment model with sequence
One-compartment model with sleep statement
One-compartment first-order absorption model, compartment initialized with sequence
One-compartment first-order absorption, closed-form
One-compartment first-order absorption with lag time, closed-form
One-compartment IV bolus with time-to-event outcome and PK observations
Multinomial (ordered categorical)
category3(){
#observed values are one of three categories 0, 1, or 2
#probability of observing a higher category number increases
#with covariate x
covariate(x)
fixef(
x1=c(0, 1.5,)
x12=c(0, 1,)
)
ranef(nx1=0.25)
stparm(xx1=x1+nx1, xx2=xx1+x12)
#xx2 > xx1 since x12 > 0
y1=x-xx1
y2=x-xx2
#xx2 > xx1, so y1 > y2
#ilogit(y)=exp(y)/(1+exp(y)), built in function
p01=ilogit(y1)
p12=ilogit(y2)
#by construction, y2<y1, so 0<p12<p01<1
#p12=prob(category2)
#p01=prob(category 2)+prob(category 1)
#1-p01=prob(category 0)
LL(y, log(y == 0 ? 1-p01:y == 1 ? p01-p12:p12-0))
}Time to event model (exponential)
Hazard model data for subject 1. Events occurred at time=1.72 and 2.43, then from 2.43 to 4.00 no event occurred (right censored). The first record with an empty observation establishes the time of the start of the first period.
## id time dose occur
1 0 10 .
1 1.72 10 1
1 2.43 10 1
1 4.00 10 0
#The above data says the event occurred at times 1.72 and
#2.43, then between times 2.43 and 4.00 it did not occur,
#so it is right-censored.
Model file:
hazard(){
covariate(dose)
fixef(
tvlHaz=c(, -2,)
dlHazdDose=c(-0.8, 1.2, 1.2)
)
stparm(haz=exp((tvlHaz+nlHaz)+dlHazdDose*dose))
ranef(nlHaz=0.01)
#The hazard function haz (which here is a constant) is
#integrated over the current period by a hidden differential
#equation dcumhazard/dt=haz, which yields a survival
#probability of S=exp(-cumhazard). That integral is reset
#to zero after every observation.
#
#The likelihood (if the event occurred) is S*haz and S (if
#an event did not occur). This likelihood computation and
#the differential equation computation are automatically
#invoked by event(occur,haz).
event(occur, haz)
}Interval censoring capabilities of the event statement are signified by observed values.
2: Indicates the end of an interval in which the event occurred one or more times but at unknown times. In this case P = 1 – S.
–1, –2, –…: Indicates the end of an interval in which the event occurred exactly n=1, or 2, or … times, where the time is unknown. In this case:
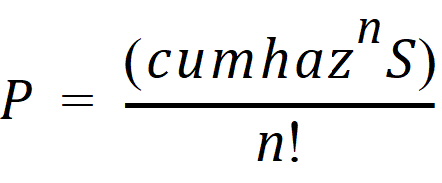
(a Poisson distribution).
Note: this is equivalent to a simple Poisson count model.
–999999: Indicates the end of an interval in which the event occurred an unknown number of times, i.e., the subject was simply out of contact with no information, so P = 1.
To model Weibull-distributed events, whether censored or not, if there is more than one event per subject, a decision must be made as to what time value to use for each observation. There are usually two possibilities:
Delta-time since prior observation (or start of subject)
Delta-time since start of subject
This section shows how to do both possibilities.
First, Weibull has two structural parameters, which will be called lambda and k in this example. lambda is the scale parameter. The larger the lambda, the larger the expected time to observation. k is the shape parameter. The larger the k, the more sigmoidal the survival function. The hazard rate is a function of these two parameters:
hazard=k/lambda*(T/lambda)^(k-1)
where T is one of the two Delta-time values mentioned above.
To follow option 1, one could say:
hazard=k/lambda*(T/lambda)^(k-1)
deriv(T=1) #take explicit control of time
deriv(cumhaz=hazard)
LL(flag, log(flag?hazard*exp(-cumhaz):
exp(-cumhaz)), doafter={cumhaz=0; T=0;})
or use the built-in event statement:
hazard=k/lambda*(T/lambda)^(k-1)
deriv(T=1)
event(occur, hazard, doafter={T=0;})
To follow option 2, one could say:
hazard=k/lambda*(T/lambda)^(k-1)
deriv(T=1)
deriv(cumhaz=hazard)
LL(occur, log(occur?hazard*exp(-cumhaz):
exp(-cumhaz)))
# Notice that t could be used in place of T, and
# deriv(T=1) could be removed.
Notice that the event statement can only be used in option 1 because it automatically resets the accumulated hazard, where in option 2, that is not desired.
Emax (Hill) model with exponent
emaxhill(){
e=e0+(emax-e0)*c^Power/(c^Power+ec50^Power)
fixef(
tvE0=c(0, 2,)
tvEMax=c(0, 5,)
tvlEC50=c(0, 1.1,)
tvPower=c(0, 1,)
)
covariate(c)
stparm(
e0=tvE0+nE0
emax=tvEMax+nEMax
ec50=exp(tvlEC50+nlEC50)
Power=tvPower #no random effect
)
ranef(nE0=1, nEMax=2, nlEC50=1)
error(eps1=2)
observe(eObs=e+eps1)
}One-compartment IV bolus population PK
ivbolus(){
dosepoint(a)
deriv(a=-a*ke)
#replace above line with “cfMicro(a, ke)” for closed form
#formulation
c=a/v
fixef(
tvlKe=c(, -4.6,)
tvlV=c(, 2.3,)
)
stparm(ke=exp(tvlKe+nlKe), v=exp(tvlV+nlV))
ranef(nlKe=0.25, nlV=0.25)
error(eps1=0.5) #initial estimate res err cv=50%
observe(cObs=c*(1+eps1)) #proportional residual error
}One-compartment IV bolus, two parallel models with common fixed effects
ivboluspar(){
dosepoint(a1)
deriv(a1=-a1*ke1)
c1=a1/v1
dosepoint(a2)
deriv(a2=-a2*ke2)
c2=a2/v2
fixef(
tvlKe=c(, -4.6,)
tvlV=c(, 2.3,)
)
ranef(block(nlKe1, nlV1)=c(0.25, 0.01, 0.25)
same(nlKe2,nlV2))
stparm(ke1=exp(tvlKe+nlKe1), v1=exp(tvlV+nlV1))
stparm(ke2=exp(tvlKe+nlKe2), v2=exp(tvlV+nlV2))
error(eps1=1)
observe(cObs1=c1+eps1)
observe(cObs2=c2+eps1)
}One-compartment model with sequence
onecompfoseq(){
deriv(a=-a*ke)
c=a/v
fixef(
tvlKe=c(, -4.6,)
tvlV=c(, 2.3,)
)
stparm(ke=exp(tvlKe+nlKe), v=exp(tvlV+nlV))
ranef(nlKe=0.5, nlV=0.5)
error(eps1=1)
observe(cObs=c+c*eps1) #proportional residual error
sequence{
a=10 #sets initial value of compartment a to 10
#useful if all subjects have a single bolus dose of 10 at
#time=0
}
}One-compartment model with sleep statement
testmodel(){
deriv(a=-a*ke)
c=a/v
fixef(
tvlKe=c(, -4.6,)
tvlV=c(, 2.3,)
)
stparm(ke=exp(tvlKe+nlKe), v=exp(tvlV+nlV))
ranef(nlKe=0.5, nlV=0.5)
error(eps1=1)
observe(cObs=c+c*eps1)
sequence {
sleep(1) #sleep for time duration=1
a=10 #set compartment a to 10 after sleep i.e., at time=1
}
}One-compartment first-order absorption model, compartment initialized with sequence
onecmtfo(){
deriv(aa=-aa*ka)
deriv(a1=aa*ka-a1*ke)
#replace above two lines with "cfMicro(aa, ke, first=
#(depot=ka))" to obtain faster closed form version
dosepoint(aa)
sequence {a1=4.8} #initializes compartment a1 to 4.8
c=a1/v
stparm(
ka=exp(tvlKa+nlKa)
ke=exp(tvlKe+nlKe)
v=exp(tvlV+nlV)
)
ranef(nlKa=0.25, nlKe=0.25, nlV=0.25)
fixef(
tvlKa=c(, -0.7,)
tvlKe=c(, -3,)
tvlV=c(, 2.3,)
)
error(eps1=1)
observe(cObs=c+eps1)
}One-compartment first-order absorption, closed-form
onecmptfocf(){
cfMicro(a1, ke, first=(aa=ka))
#aa is an arbitrary name of the depot (dosing) compartment -
#not used elsewhere in the model.
dosepoint(aa)
c=a1/v
stparm(
ka=exp(tvlKa+nlKa)
ke=exp(tvlKe+nlKe)
v=exp(tvlV+nlV)
)
ranef(nlKa=0.25, nlKe=0.25, nlV=0.25)
fixef(
tvlKa=c(, -0.7,)
tvlKe=c(, -3,)
tvlV=c(, 2.3,)
)
error(eps1=1)
observe(cObs=c+c*eps1)
}One-compartment first-order absorption with lag time, closed-form
onecmptfolag(){
dosepoint(aa, tlag=tlag)
cfMicro(aa,ke,first=(depot=ka))
#faster evaluation than equivalent ODE system
#deriv(aa=-aa*ka)
#deriv(a1=aa*ka-a1*ke)
c=a1/v
stparm(
ka=exp(tvlKa+nlKa)
tlag=exp(tvlTLag+nlTLag)
ke=exp(tvlKe+nlKe)
v=exp(tvlV+nlV)
)
ranef(nlKa=0.25, nlTLag=0.25, nlKe=0.25, nlV=0.25)
fixef(
tvlKa=c(, 1,)
tvlTLag=c(, 0.1,)
tvlKe=c(, -3,)
tvlV=c(, 2.3,)
)
error(eps1=1)
observe(cObs=c+c*eps1)
}One-compartment IV bolus with time-to-event outcome and PK observations
timetoeventconc(){
dosepoint(a)
deriv(a=-a*ke)
c=a/v
fixef(
tvlKe=c(, -4.6,)
tvlV=c(, 2.3,)
dHdC=c(0, 0.01,)
)
stparm(ke=exp(tvlKe+nlKe), v=exp(tvlV+nlV))
ranef(nlKe=0.5, nlV=0.5)
error(eps1=1)
observe(cObs=c+c*eps1)
#instantaneous hazard rate is assumed proportional to
#concentration c
#proportionality constant dHdC is a fixed effect to be
#estimated
event(occur, c*dHdC)
}