The Engine Settings tab provides control over the model fitting algorithm and related settings.
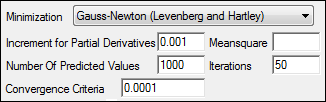
Use the Minimization menu to select the method to use with the Indirect Response model.
Method 1: The Nelder-Mead algorithm does not require the estimated variance-covariance matrix as part of its algorithm, so it often performs very well on ill-conditioned datasets. Ill-conditioned indicates that, for the given dataset and model, there is not enough information contained in the data to precisely estimate all of the parameters in the model or that the sum of squares surface is highly curved. Although the procedure works well, it can be slow, particularly when used to fit a system of differential equations.
Method 2: Gauss-Newton (Levenberg and Hartley) is the default algorithm and performs well on a wide class of problems, including ill-conditioned datasets. Although the Gauss-Newton method does require the estimated variance-covariance matrix of the parameters, the Levenberg modification suppresses the magnitude of the change in parameter values from iteration to iteration to a reasonable amount. This enables the method to perform well on ill-conditioned datasets.
Method 3: Gauss-Newton (Hartley) is another Gauss-Newton method. It is not as robust as Methods 1 and 2 but is extremely fast. Method 3 is recommended when speed is a consideration or when maximum likelihood estimation or linear regression analysis is to be performed. It is not recommended for fitting complex models.
Note: The use of bounds is recommended with Methods 2 and 3. For linear regressions, use Method 3 without bounds.
In the Increment for Partial Derivatives text field, type the incremental value that the parameter value is to be multiplied by.
Nonlinear algorithms require derivatives of the models with respect to the parameters. The program estimates these derivatives using a difference equation. For example (D = the increment with which the parameter value is multiplied)
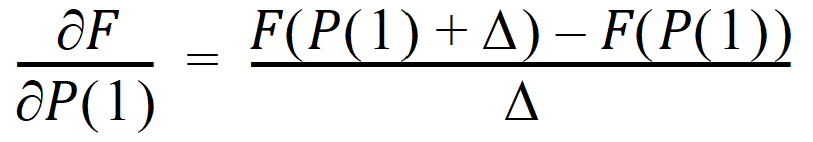
In the Number of Predicted Values text field, type the number of predicted values used to determine the number of points in the predicted data.
Use this option to create a dataset that will plot a smooth curve. When fitting or simulating multiple dose data, the predicted data plots may be much improved by increasing the number of predicted values. The minimum allowable value is 10; the maximum is 20,000.
If the number of derivatives is greater than zero (i.e., differential equations are used), this command is ignored and the number of predicted points is equal to the number of points in the dataset.
For compiled models without differential equation, the default value is 1000. The default for user models is the number of data points in the original dataset. This value may be increased only if the model has no more than one independent variable.
Note: To better reflect peaks (for IV dosing) and troughs (for extravascular, IV infusion and IV bolus dosing), the predicted data for the built-in PK models includes dosing times, in addition to the concentrations generated. For all three types, concentrations are generated at dosing times; in addition, for infusion models, data are generated for the end of infusion.
In the Convergence Criteria text field, type the criterion value used to determine convergence.
The default is 0.0001. Convergence is achieved when the relative change in the residual sum of squares is less than the convergence criterion.
Leave the Meansquare text field blank, unless the mean square needs to be a fixed value in order to compute the variance in a model.
The variance is normally a function of the weighted residual SS/df, or the Mean Square. For certain types of problems, when computing the variance, the mean square needs to be set to a fixed value.
Leave the Iterations text field set to its default value, unless the purpose of the model is to evaluate it, and not fit it.
The default iteration values are:
500 for Nelder-Mead minimization. Each iteration is a reflection of the simplex.
50 for Gauss-Newton (Levenberg and Hartley) or Gauss-Newton (Hartley) minimizations.
Type a value of 0 (zero) in the Iterations text field if the purpose of the model is evaluation.
A value of 0 requires that initial parameter values be user-specified and all output will use the initial estimates as the final parameters.