The two-period crossover design is common for clinical trials in which each subject serves as his or her own control. In many situations the assumptions of variance homogeneity and normality, relied upon in parametric analyses, may not be justified due to small sample size, among other reasons. The nonparametric methods proposed by Koch (1972) (The use of nonparametric methods in the statistical analysis of the two-period change-over design. Biometrics 577–83.) can be used to analyze such data.
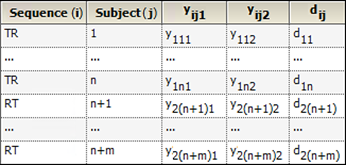
Consider a trial testing the effects of two treatments, Test (T) and Reference (R). Suppose that n subjects are randomly assigned to the first sequence, TR, in which subjects are given treatment T first and then treatment R following an adequate washout period. Similarly, m subjects are assigned to the RT sequence. Y represents the outcome of the trial (for example Cmax or Tmax) and yijk is the value observed on sequence i (i=1,2), subject j (j = 1,2,…,n, n+1,…n+m) and period k (k=1,2). Treatment is implied by sequence i and period k, for example i=1 and k=1 is treatment T; i=1 and k=2 is treatment R. The data are listed in columns 1 through 4 of the following table, and column 5 gives the within-subject difference in Y between the two periods, where:
dij = yij1 – yij2
Then the n*m crossover differences (d1i – d2j)/2 are computed, along with the median of these n*m points. This median is the Hodges-Lehmann estimate of the difference between the median for T and the median for R.
Crossover Design supports two data layouts: stacked in same column or separate columns. For “stacked” data, all measurements appear in a single column, with one or more additional columns flagging which data belong to which treatment. The data for one treatment must be listed first, then all the data for the other. The alternative is to place data for each treatment in a separate column.
The median response and its interval are calculated for Y of each treatment and the crossover difference between treatments, C. Let X(1), X(2),…, X(N) be the order statistic of samples X1, X2,…, XN. The median Xm is defined as:
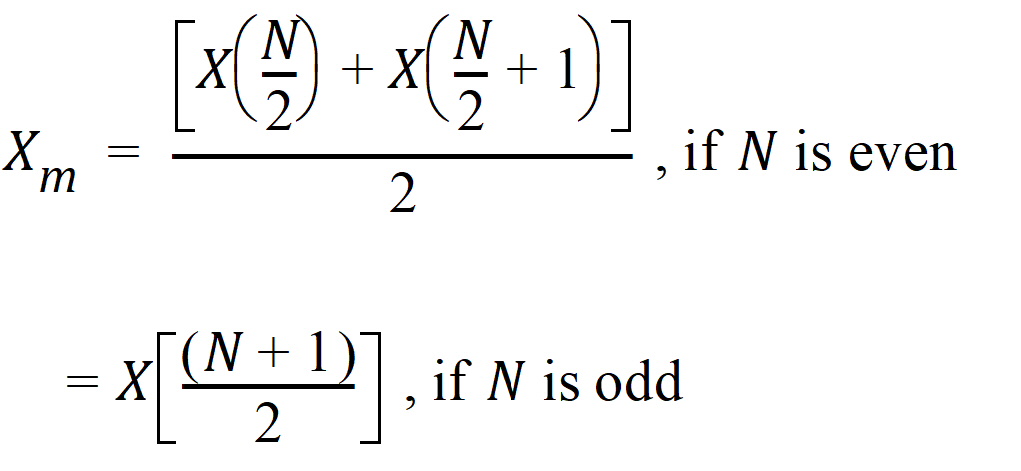
The 100% confidence interval (CI) of Xm is defined as follows.
For N <= 20, the exact probability value is obtained from a Mann-Whitney U-distribution.
For N > 20, normal approximation is used:
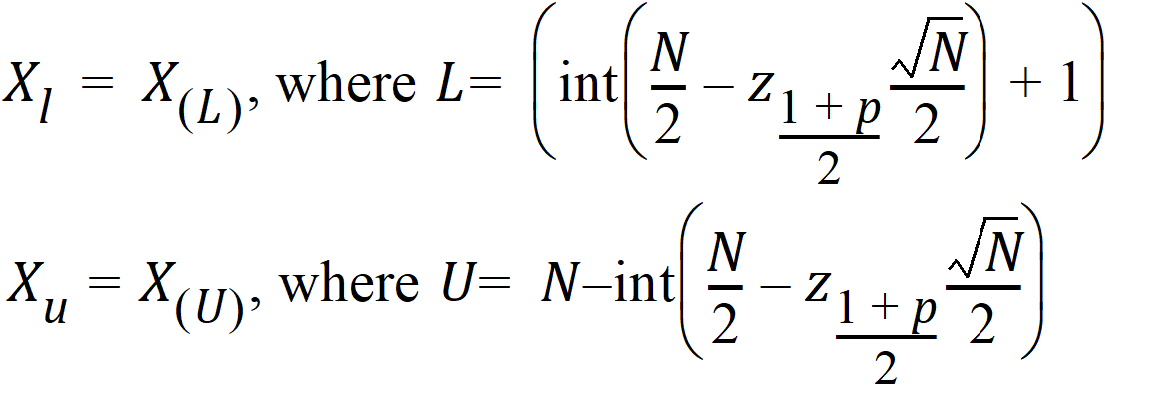
where int(X) returns the largest integer less than or equal to X.
Four hypotheses are of interest:
no sequence effect (or drug residual effect);
no treatment effect given no sequence effect;
no period effect given no sequence effect; and
no treatment and no sequence effect.
Hypothesis 1 above can be tested using the Wilcoxon statistic on the sum S. If R(Sl) is the rank of Sij in the whole sample, l = 1,…, n+m. The test statistic is:
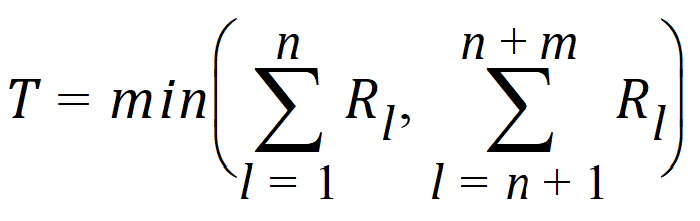
The p-value is evaluated by using normal approximation (Conover, 1980):
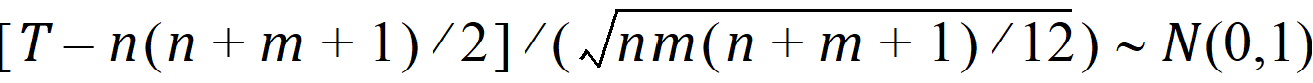
Similarly, hypothesis 2 can be tested using the Wilcoxon statistic on the difference D; hypothesis 3 can be tested using the Wilcoxon statistic on the crossover difference C. The statistics are in the form described above.
Hypothesis 4 can be tested using the bivariate Wilcoxon statistic on (Yij1, Yij2). For each period k, let Rijk equal:
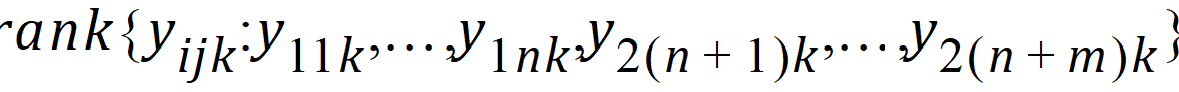
The average rank for each sequence is:
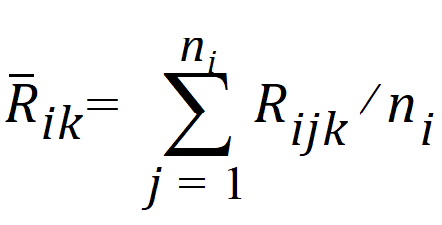
where j=1,…, ni, ni=n for i=1, and ni=m for i=2
Thus, the statistic to be used for testing hypothesis 4 is:
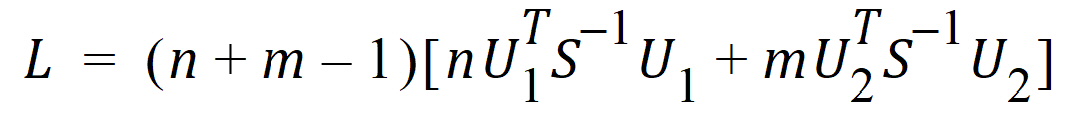
where Ui is a 2x1 vector:
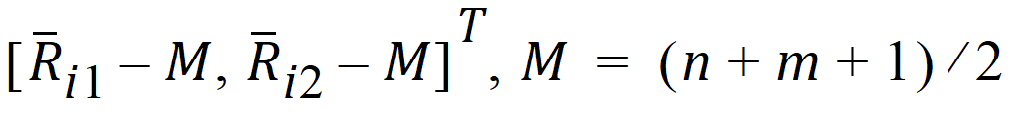
S is the 2x2 covariance matrix:
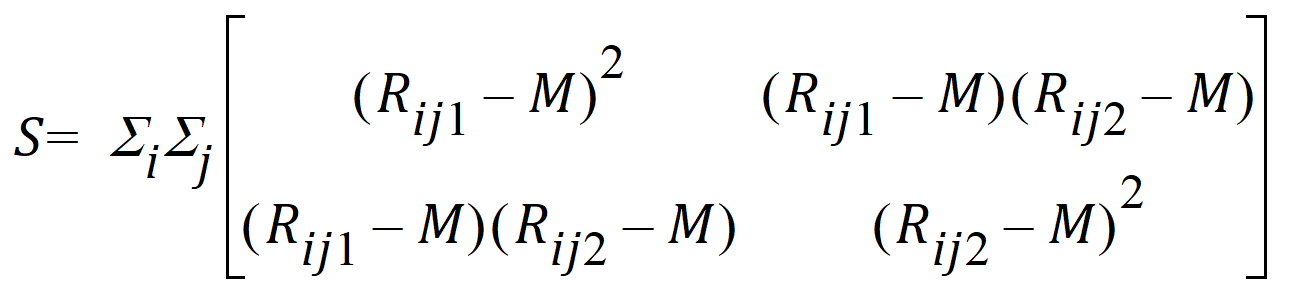
and L ~ X2, so the p-value can be evaluated.
Conover (1980). Practical Nonparametric Statistics 2nd ed. John Wiley & Sons, New York.
Dixon and Massey (1969). Introduction to Statistical Analysis, 3rd ed. McGraw-Hill Book Company, New York.
Koch (1972). The use of non-parametric methods in the statistical analysis of the two-period change-over design. Biometrics 577–84.
Kutner (1974). Hypothesis testing in linear models (Eisenhart Model 1). The American Statistician, 28(3):98–100.
Searle (1971). Linear Models. John Wiley & Sons, New York.
Steel and Torrie (1980). Principles and Procedures of Statistics; A Biometrical Approach, 2nd ed. McGraw-Hill Book Company, New York.
Winer (1971). Statistical Principles in Experimental Design, 2nd ed. McGraw-Hill Book Company, New York, et al.