The Phoenix Convolution tool supports analytic evaluation of the convolution integral,
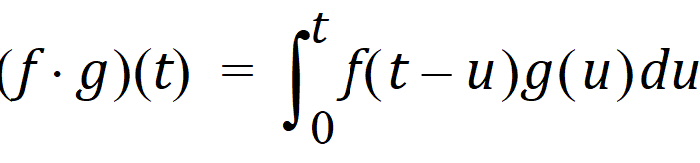
where f(t) and g(t) are constrained to be either polyexponentials or piecewise polynomials (splines), in any combination. Polyexponentials must take the form:
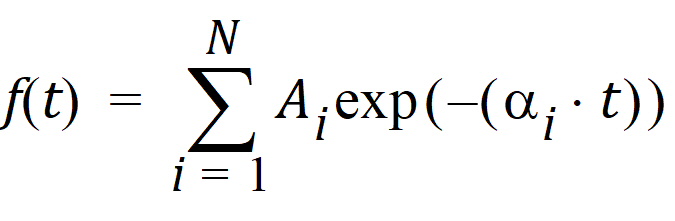
where N <= 9 and t >= 0. To specify a polyexponential, you must supply the polyexponential coefficients, i.e., the A and alpha.
Splines must be piecewise constant or linear splines, i.e., they must take the form:
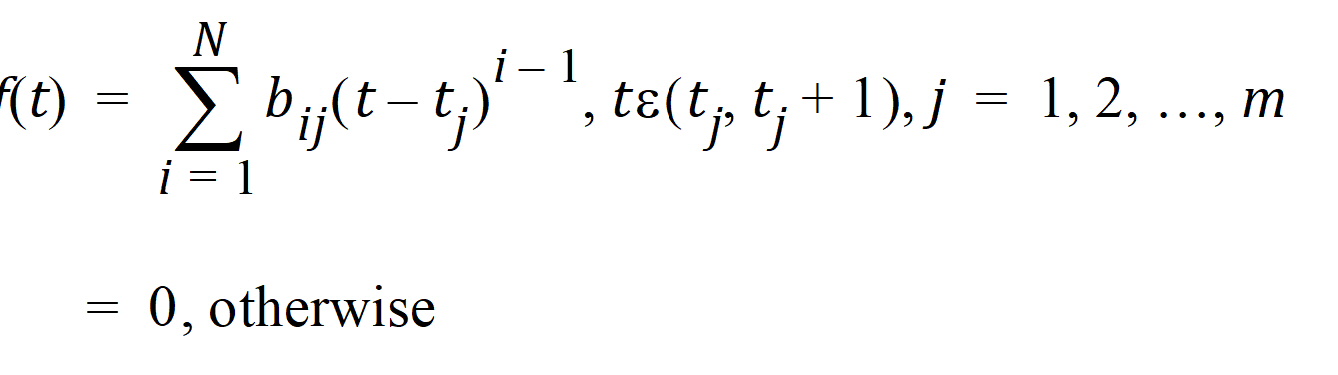
where N is restricted to be 1 or 2.
For a spline function, you must supply a dataset to be fit with the splines. You can choose to convolve either this spline function, e.g., input rate data, or the derivative of this spline function, e.g., cumulative input data. For the first case, the Convolution tool will find the spline with the requested degree of polynomial splines, and will use these polynomial splines in the convolution. For the derivative of a spline, the Convolution tool will fit the data with the requested degree of polynomial splines, differentiate the splines to obtain polynomial splines of one degree lower, and use the derivatives in the convolution. For example, if cumulative input data is fit with linear splines, then the derivatives are piecewise constant, so the piecewise constant function is convolved with the other specified function.
Linear splines are the lines that connect the (x,y) points. For t e (ti, ti+1),
y = yi + mi(t – ti)
where mi is the slope:
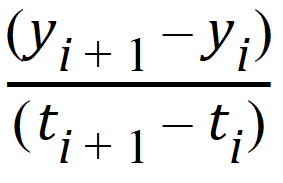
The derivative of a linear spline function is a piecewise constant function, with the constants being the slopes mi. For input rate data, each piecewise constant spline will have the value that is the average of the y-values of the endpoints. This option is not available for cumulative input data since the derivative will be zero.