Population and individual bioequivalence

Population and individual bioequivalence are used to assess switchability and prescribability. Because individual bioequivalence relies on estimates of within-subject, within-formulation variation, replicated crossover designs are required. This algorithm was developed by Francis Hsuan. Designs that can be appropriately analyzed include, but are not limited to the following list, which shows the Sequence (Period) Design.

2 (4) TRTR/RTRT
4 (4) TRTR/RTRT/TRRT/RTTR
4 (2) TT/RR/TR/RT
4 (3) TRT/RTR/TRR/RTT
2 (5) TRRTT/RTTRR
3 (3) TRR/RTR/RRT
2 (3) RTR/TRT
6 (3) TRR/RTT/TRT/RTR/TTR/RRT
2 (4) TRRR/RTTT
6 (4) TTRR/RRTT/TRRT/RTTR/TRRR/RTTT

The algorithm works for balanced and unbalanced data with an equal number of periods in each sequence and one measurement per subject in each period.

Bioequivalence criterion
Computational details

Bioequivalence criterion

Population bioequivalence (PBE) criteria are:

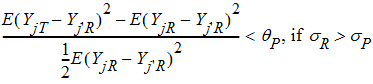
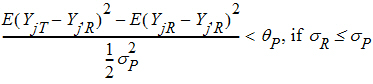
where s_P defaults to 0.2 and q_P=(ln(1 – PercentReference)+e_P) /s_P². The default value for PercentReference is 0.20. In the Bioequivalence object, s_P is called the Total SD standard. s_R²is computed by the program and is the total variance of the reference formulation, i.e., the sum of within- and between-subject variance. The criteria take the linearized form:

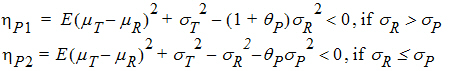
Individual bioequivalence (IBE) criteria are:

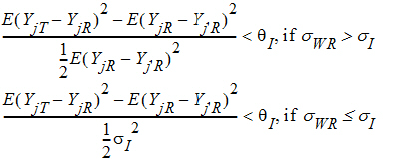
where s_I defaults to 0.2 and q_I=(ln(1 – PercentReference)+e_I) /s_I². The default value for Percent Reference is 0.20, and the default value for e_I is 0.05. In the Bioequivalence object, s_I is called the within-subject SD standard. s_WR is computed by Phoenix, and its square, s_WR², is the within-subject variance of the reference formulation.

The IBE criteria take the linearized form:

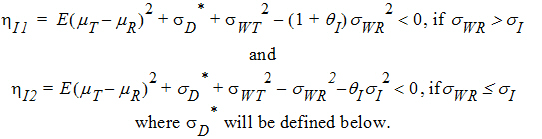
For reference scaling, use h_P1 or h_I1. For constant scaling, use h_P2 or h_I2. For mixed scaling, use one of the following.

Population

If s_R > s_Pv, use h_P1
If s_R £ s_P, use h_P2

Individual

If s_WR > s_I, useh_I1
If s_WR £ s_I, use h_I2

If the upper bound on the appropriate h is less than zero, then the product is bioequivalent in the chosen sense. The interval is set in the Bioequivalence object’s Options tab. The method of calculating that upper bound follows.

Computational details

Let:

Y_ijkt be the response of subject j in sequence i at time t with treatment k.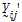
be a vector of responses for subject j in sequence i. The components of Y are arranged in the ascending order of time.
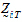.be the design vector of treatment T in sequence i.
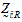be a design vector for treatment R in sequence i.
n_i > 1 be the number of subjects in sequence i.

Assume the mean responses of 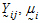, follow a linear model:

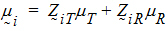
where m_T, m_R are the population mean responses of Y with treatments T and R respectively, and X_iare design/model matrices.

Let:

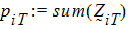
be the number of occasions T is assigned to the subjects in sequence i.

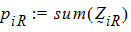
be the number of occasions R is assigned to the subjects in sequence i.

Then:

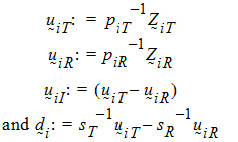
Assume that the covariances:

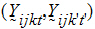
follow the model:

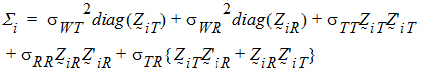
where the parameters:

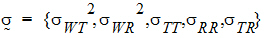
are defined as follows:

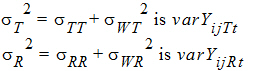
intra-subject correlation coefficients are:

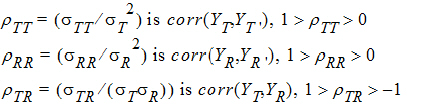
intra-subject covariances are:

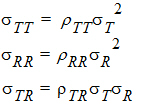
intra-subject variances are:

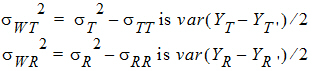
For PBE and IBE investigations, it is useful to define additional parameters:

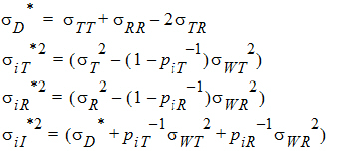
Except for s_D^*, all the quantities above are non-negative when they exist. It satisfies the equation:

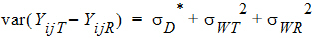
In general, this s_D^* may be negative. This method for PBE/IBE is based on the multivariate model. This method is applicable to a variety of higher-order two-treatment crossover designs including TR/RT/TT/RR (the Balaam Design), TRT/RTR, or TxRR/xRTT/RTxx/TRxx/xTRR/RxTT (Table 5.7 of Jones and Kenward, page 205).

Given the i^th sequence, let:

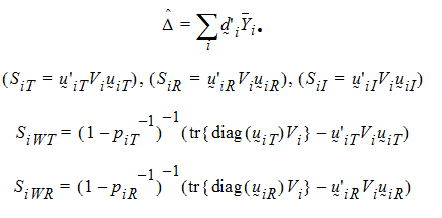
where: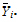
is the sample mean of the i^th sequence.
V_i is the within-sequence sample covariance matrix.

It can be shown that:

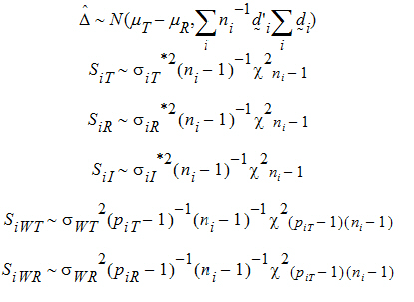
Furthermore, it can be shown that {S_iT, S_iR} (for PBE) are statistically independent from {D} and {S_iWT, S_iWR}, and that the four statistics D, S_iI, S_iWT, S_iWR (for IBE) are statistically independent.

Let a_i be sets of normalized weights, chosen to yield the method of moments estimates of the h. Then define the estimators of the components of the linearized criterion by:

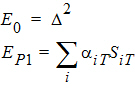
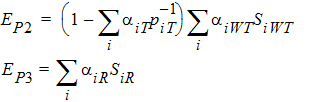
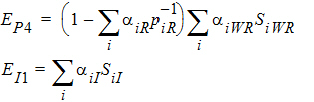
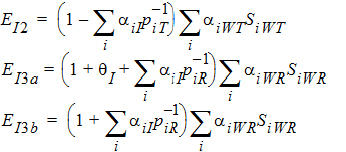
Using the above notation, one may define unbiased moment estimators for the PBE criteria:

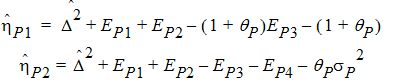
and for the IBE criteria:

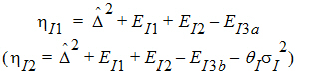
Construct a 95% upper bound for h based on the TRTR/RTRT design using Howe’s approximation I and a modification proposed by Hyslop, Hsuan and Holder (2000). This can be generalized to compute the following sets of n_q, H, and U statistics:

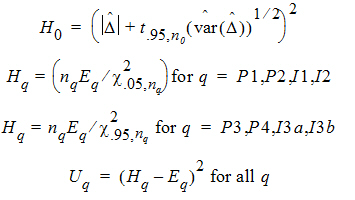
where the degrees of freedom n_q are computed using Satterthwaite’s approximation. Then, the 95% upper bound for each h is:

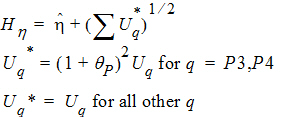
If H_q < 0, that indicates bioequivalence; H_q > 0 fails to show bioequivalence.

References

Anderson and Hauck (1983). A new procedure for testing equivalence in comparative bioavailability and other clinical trials. Commun Stat Theory Methods, 12:2663–92.

Chow and Liu (2nd ed. 2000 or 3rd ed. 2009). Design and Analysis of Bioavailability and Bioequivalence Studies, Marcel Dekker, Inc.

Hauschke, Steinijans, Diletti, Schall, Luus, Elze and Blume (1994). Presentation of the intrasubject coefficient of variation for sample size planning in bioequivalence studies. Int J Clin Pharm Ther 32(7): 376–378.

Hyslop, Hsuan and Holder (2000). A small sample on interval approach to assess individual bioequivalence. Statist Medicine 19:2885–97.

Schuirmann (1987). A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability. J Pharmacokinet Biopharm 15:657–680.

Snedecor and Cochran (1989). Statistical Methods, 8th edition, Iowa State Press.

US FDA Guidance for Industry (March 2003). Bioavailability and Bioequivalence Studies for Orally Administered Drug Products—General Considerations.

US FDA Guidance for Industry (January 2001). Statistical Approaches to Establishing Bioequivalence.

Phillips, K. F. (1990). Power of the Two One-Sided Tests Procedure in Bioequivalence. Journal of Pharmacokinetics and Biopharmaceutics 18: 137–144.

Diletti, E., Hauschke, D., and Steinijans, V. W. (1991). Sample size determination for bioequivalence assessment by means of intervals. Int. J. of Clinical Pharmacology, Therapy and Toxicology 29: 1–8.

Owen, D. B. (1965). A Special case of a bivariate noncentral t-distribution. Biometrika 52: 437–446.