PK Models

Pharmacokinetic models

Phoenix includes nineteen pharmacokinetic (PK) models. Each is available in the PK Model object.

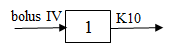
Model 1: IV-bolus input, 1-compartment, no lag, 1st order elimination
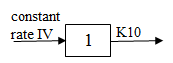
Model 2: IV-infusion input, 1-compartment, no lag, 1st order elimination
Model 3 1st order input, 1-compartment, no lag, 1st order elimination
Model 4 1st order input, 1-compartment, yes lag, 1st order elimination
Model 5 1st order input, 1-compartment, K10=K01 parameterization, no lag, 1st order elimination
Model 6 1st order input, 1-compartment, K10=K01 parameterization, yes lag, 1st order elimination
Model 7 IV-bolus input, 2-compartment, micro parameterization, no lag, 1st order elimination
Model 8 IV-bolus input, 2-compartment, macro parameterization, no lag, 1st order elimination
Model 9 IV-infusion input, 2-compartment, micro parameterization, no lag, 1st order elimination
Model 10 IV-infusion input, 2-compartment, macro parameterization, no lag, 1st order elimination
Model 11 1st order input, 2-compartment, micro parameterization, no lag, 1st order elimination
Model 12 1st order input, 2-compartment, micro parameterization, yes lag, 1st order elimination
Model 13 1st order input, 2-compartment, macro parameterization, no lag, 1st order elimination
Model 14 1st order input, 2-compartment, macro parameterization, yes lag, 1st order elimination
Model 15 IV-bolus + IV-infusion input, 1-compartment, micro parameterization, no lag, 1st order elimination
Model 16 IV-bolus + IV-infusion input, 2-compartment, micro parameterization, no lag, 1st order elimination
Model 17 IV-bolus + IV-infusion input, 2-compartment, macro parameterization, no lag, 1st order elimination
Model 18 IV-bolus input, 3-compartment, macro parameterization, no lag, 1st order elimination
Model 19 IV-infusion input, 3-compartment, macro parameterization, no lag, 1st order elimination

Note:All models except models 15–17 accept multiple dose data.

The models shown in this section give equations for compartment 1 (central).

Model 1

One-compartment with IV-bolus input and first-order output.

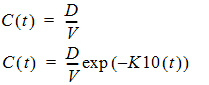
Required constants: N doses, dose N, time of dose N (Repeat for each dose)
Estimated parameters: V (volume), K10 (elimination rate)
Secondary parameters: AUC=D/V/K10, K10 half-life, Cmax=D/V, AUMC, MRT, Vss
Clearance estimated: V, CL
Clearance secondary: AUC, K10 half-life, Cmax, AUMC, MRT, VSS

Model 2

One-compartment with constant IV input, first-order absorption.

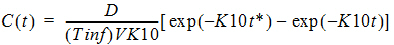
where:

Tinf = infusion length
t* = t – Tinf for t > Tinf
t* = 0 for t £ Tinf

Required constants: N doses, dose N, start time N, end time N (Repeat for each dose)
Estimated parameters: V (volume), K10 (elimination rate)
Secondary parameters: AUC=D/V/K10, K10 half-life, Cmax=C(Tinf), CL, AUMC, MRT, Vss
Clearance estimated: V, CL
Clearance secondary: AUC, K10 half-life, Cmax, K10, AUMC, MRT, VSS

Model 3

One-compartment with first-order input and output, no lag time.

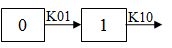
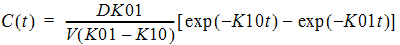
Required constants: N doses, dose N, time of dose N (Repeat for each dose)
Estimated parameters: V_F, K01 (absorption rate), K10 (elimination rate)
Secondary parameters: AUC=D/V/K10, K01 half-life, K10 half-life, CL_F, Tmax=time of Cmax = [ln(K01/K10)] / [(K01 – K10)]
Clearance estimated: V_F, K01, CL_F
Clearance secondary: AUC, K01 half-life, K10 half-life, K10, Tmax, Cmax

Model 4

One-compartment with first-order input and output with lag time.

Identical to Model 3, with an additional estimated parameter: Tlag=lag time. In the Model 3 equation, substitute (t - Tlag) for t.

Model 5

One-compartment, equal first-order input and output, no lag time.

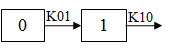
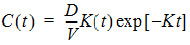
Required constants: N doses, dose N, time of dose N (Repeat for each dose)
Estimated parameters: V_F, K (absorption and elimination rate)
Secondary parameters: AUC=D/V/K, K half-life, CL_F, Tmax=time of Cmax=1/K
Clearance estimated: V_F, CL_F
Clearance secondary: AUC, K half-life, K, Tmax, Cmax

Model 6

One-compartment, equal first-order input and output with lag time.

Identical to Model 5, with an additional estimated parameter: Tlag=lag time. In the Model 5 equation, substitute (t - Tlag) for t.

Model 7

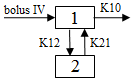
Two-compartment with bolus input and first-order output; micro-constants as primary parameters.

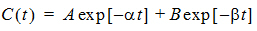
where:

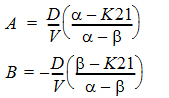
–a and –b (a > b) are the roots of the quadratic equation:
r² + (K12 + K21 + K10)r + K21(K10) = 0

Required constants: N doses, dose N, time of dose N, (Repeat for each dose)
Estimated parameters: V1 is Volume1, K10 (elimination rate), K12 (transfer rate, 1 to 2), K21 (transfer rate, 2 to 1)
Secondary parameters: AUC=A/Alpha+B/Beta, K01 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, Cmax=D/V, CL, AUMC, MRT, Vss, V2, CLD2
Clearance estimated: V1, CL, V2, CLD2
Clearance secondary: AUC, K10 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, Cmax, K10, AUMC, MRT, Vss, K12, K21

Model 8

Two-compartment with bolus input and first-order output; macro-constants as primary parameters.

As Model 7 with macroconstants as the primary (estimated) parameters. Clearance parameters are not available for Model 8.

Required constants: Stripping dose, N doses, dose N, time of dose N (Repeat for each dose)
Estimated parameters: A, B, Alpha, Beta
Secondary parameters: AUC=A/Alpha+B/Beta, K10 half-life, Alpha half-life, Beta half-life, K10, K12, K21, Cmax, V1, CL, AUMC, MRT, Vss, V2, CLD2

Model 9

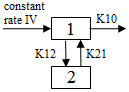
Two-compartment with constant IV input and first-order output; micro-constants as primary parameters.

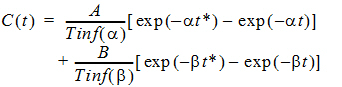
where:

Tinf = infusion length
t* = t – Tinf for t > Tinf
t* = 0 for t £ Tinf

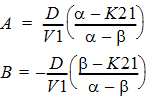
–a and –b (a > b) are the roots of the quadratic equation:
r² + (K12 + K21 + K10)r + K21(K10) = 0

Required constants: N doses, dose N, start time N, end time N,
Estimated parameters: V1 is Volume1, K10 (elimination rate), K12 (transfer rate, 1 to 2), K21 (transfer rate, 2 to 1) (Repeat for each dose)
Secondary parameters: AUC=D/V/K10, K10 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, Cmax=C(T_inf), AUMC, MRT, Vss, V2, CLD2
Clearance estimated: V1, CL, V2, CLD2,
Clearance secondary: AUC, K10 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, Cmax, AUMC, MRT, Vss, K12, K21

Model 10

Two-compartment with constant IV input and first-order output; macro-constants as primary parameters.

As Model 9 with macroconstants as the primary (estimated) parameters. Clearance parameters are not available in Model 10.

Required constants: N doses, dose N, start time N, end time N (Repeat for each dose)
Estimated parameters: V1, K21, Alpha, Beta
Secondary parameters: K10, K12, K10 half-life, AUC, Alpha half-life, Beta half-life, A, B, Cmax, CL, AUMC, MRT, Vss, V2, CLD2

Model 11

Two-compartment with first-order input, first-order output, no lag time and micro-constants as primary parameters.

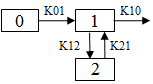
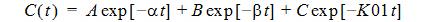
where:

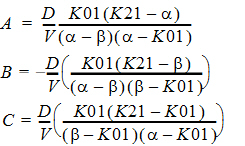
–a and –b (a > b) are the roots of the quadratic equation:
r² + (K12 + K21 + K10)r + K21(K10) = 0

Required constants: N doses, dose N, time of dose N (Repeat for each dose)
Estimated parameters: V1_F, K01 (absorption rate), K10 (elimination rate), K12 (transfer rate, 1 to 2). K21 (transfer rate, 2 to 1)
Secondary parameters: AUC=D/V/K10, K01 half-life, K10 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, CL_F, V2_F, CLD2_F, Tmax^a, Cmax^a
Clearance estimated: V1_F, K01, CL_F, V2_F, CLD2_F
Clearance secondary: AUC, K01 half-life, K10 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, K10, K12, K21, Tmax, Cmax

^aEstimated for the compiled model only

Model 12

Two-compartment with first-order input, first-order output, lag time and micro-constants as primary parameters.

As Model 11, with an additional estimated parameter: Tlag=lag time. In the Model 11 equation, substitute (t - Tlag) for t.

Model 13

Two-compartment with first-order input, first-order output, no lag time and macro-constants as primary parameters.

As Model 11, with macroconstants as the primary (estimated) parameters. Clearance parameters are not available for Model 13.

Required constants: Stripping dose, N doses, dose N, time of dose N (Repeat for each dose)
Estimated parameters: A, B, K01 (absorption rate), Alpha, Beta, Note: C=–(A+B)
Secondary parameters: K10, K12, K21, AUC=D/V/K10, K01 half-life, K10 half-life, Alpha half-life, Beta half-life, V1_F, CL_F, V2_F, CLD2_F, Tmax^a, Cmax^a

^aEstimated for the compiled model only

Model 14

Two-compartment with first-order input, first-order output, lag time and macro-constants as primary parameters.

As Model 13, with an additional estimated parameter: Tlag=lag time. In the Model 3 equation, substitute (t - Tlag) for t.

Model 15

One-compartment with simultaneous bolus IV and constant IV infusion.

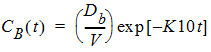
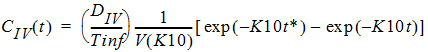
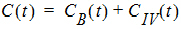
where:

Tinf = infusion length
t* = t – Tinf for t > Tinf
t* = 0 for t £ Tinf

Model 16

Two-compartment with simultaneous bolus IV and constant infusion input; micro constants as primary parameters.

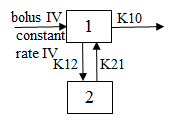
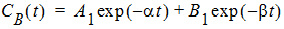
where:

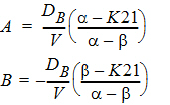
and

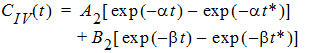
where:

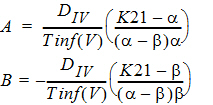
Tinf = infusion length
t* = t – Tinf for t > Tinf
t* = 0 for t £ Tinf

–a and –b (a > b) are the roots of the quadratic equation:
r² + (K12 + K21 + K10)r + K21(K10) = 0

Required constants: Bolus dose, IV dose, length of infusion (= Tinf)
Estimated parameters: V1, K10, K12, K21
Secondary parameters: K10 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, CL, V2, CLD2
Clearance estimated: V1, CL, V2, CLD2
Clearance secondary: K10 half-life, Alpha, Beta, Alpha half-life, Beta half-life, A, B, K10, K12, K21

Model 17

Two-compartment with simultaneous bolus IV and constant infusion input and macro constants as primary parameters.

As Model 10 with macroconstants as the primary (estimated) parameters.

Required constants: Stripping dose, bolus dose, IV dose, length of infusion (= Tinf)
Estimated parameters: A, B, Alpha, Beta
Secondary parameters: K10, K12, K21, K10 half-life, Alpha half-life, Beta half-life, V1, CL, V2, CLD2

Clearance parameters are not available in Model 17.

Model 18

Three-compartment with bolus input, first-order output; macro constants as primary parameters.

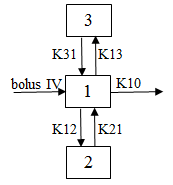
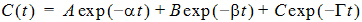
Required constants: Stripping dose, N doses, dose N, time of dose N (Repeat for each dose)
Estimated parameters: A, B, C, Alpha, Beta, Gamma
Secondary parameters: Cmax, V1, K21, K31, K10, K12, K13, K10 half-life, Alpha half-life, Beta half-life, Gamma half-life, AUC, CL, AUMC, MRT, Vss, V2, CLD2, V3, CLD3

Clearance parameters are not available in Model 18.

Model 19

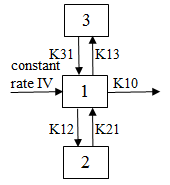
Three compartment model with constant IV infusion; macro constants as primary parameters.

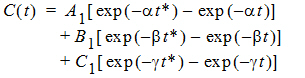
where:

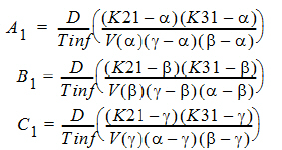
Tinf = infusion length
t* = t – Tinf for t > Tinf
t* = 0 for t £ Tinf

Required constants: N doses, dose N, start time and end time of dose N (Repeat for each dose)
Estimated parameters: V1, K21, K31, Alpha, Beta, Gamma
Secondary parameters: Cmax, K10, K12, K13, A, B, C, K10 half-life, Alpha half-life, Beta half-life, Gamma half-life, AUC, CL, AUMC, MRT, Vss, V2, CLD2, V3, CLD3

A, B, and C are the zero time intercepts following an IV injection.

Clearance parameters are not available in Model 19.