Three category multinomial model with a covariate
For this example, a completed project will be used as an illustration.
This example shows a three category multinomial model with a covariate, run with three different engines: QRPEM, Laplace, and AdaptiveGaussianQuadrature. This project illustrates how to construct such a model with the simple LL statement. It also demonstrates that the accurate methods (QRPEM and AGQ) get virtually identical and “correct” results, in good agreement with the simulation that created the data set, while the approximate method (Laplacian) gets relatively poor results that are quite different.
Information about the example data
-
Select File > Load Project to open an existing Phoenix project.
-
In the Load Project dialog, navigate to …\Examples\NLME.
-
Select Multinomial_3cat_with_covariates.phxproj and click Open.
The data set consists of simulated data from a multinomial categorical model, where the observations are either y=0,1, or 2 and represent a category. The probability of an observation being a particular category is a function of four structural parameters th1, th2, th4, and th5 as follows:
Prob(y=0)=ilogit(th1+th4*PER+th5*DOSE)
Prob(y=1)=ilogit(th1+th4*PER+th5*DOSE+th2) – Prob(category=0)
Prob(y= 2)=1 – (Prob(y=1)+Prob(y=0))
Here ilogit(x)=exp(x)/(1+exp(x)) is an increasing function of its argument.
The covariate PER (period) can take the value zero or one and can vary within an individual on different occasions. Similarly, the covariate DOSE ranges from zero to 30 and can vary within an individual.
The four structural parameters have the form th1=tvth1+nh1, th2=tvth2, th4=tvth4, and th5=tvth5, where nh1 is a N(0,20) random effect associated with th1 and the nominal values of the fixed effects are: tvth1=10, tvth2=1.5, tvth4= –5, tvth5= –0.01. (These nominal values, along with the N(0,20) distribution for nh1, were used to simulate the data).
Project workflows and objects
The techniques for constructing such a multinomial model are discussed previously in the example “Logistic regression modeling in Phoenix”.
Here the focus is on the very different results from three different types of methods depending on whether the method uses an low or high accuracy likelihood approximation.
There are three workflows in the model, as well as a Model Comparison object. The workflows correspond to running exactly the same model with the QRPEM engine, a Laplacian engine, and an adaptive Gaussian quadrature engine with 21 integration points along the one-dimension random effect nh1 axis.
-
The QRPEM method uses 300 quasi-random sample points for its evaluation of the Bayesian posterior integrals, and thus can be considered a high accuracy method.
-
The Laplacian engine uses only one integration point and is often a relatively low accuracy method, particularly in cases where the observations are categorical or counts.
-
The Adaptive Gaussian Quadrature engine with 21 points placed at particularly informative points is also a high accuracy method.
Note that Laplacian can be considered a special case of AGQ where only one integration point is used. In fact, the only difference between the Laplacian and AGQ21 workflows is that in the N AGQ box in the Run Options tab, the value is set to 21 for AGQ21 and to 1 for Laplacian.
Results
The results are summarized in the table below (most values are shown rounded to the nearest hundredth):
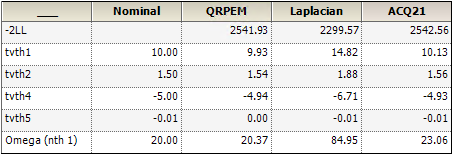
These three engines use different methods to approximate -2LL. So -2LL values cannot be used to determine which engine is better than the others. From the table above, we can see that QRPEM and AGQ21 get very good (close to nominal) estimates for all fixed effects, while the Laplacian is significantly poorer on all but Tvth5. Finally, the single random effect parameter is Omega and is estimated very well (close to the nominal value of 20) by QRPEM and AGQ21, whereas the Laplacian estimate is very poor.
