Example - Simple PK population analysis using QRPEM

Simple PK population analysis using QRPEM

This example shows how to perform a simple PK population analysis with the QRPEM engine, including dataset importation, model set up, and execution for a simple one-compartment model with parameter Cl (Clearance) and V (Volume).

Data and dosing information are assumed already collected for each patient and entered into a data file (model1pkcl.csv).

Also assumed available, using either prior information or tools like non-compartmental analysis or graphical tools in Phoenix, are initial values for the population mean of Cl and V. These will be needed by the model.

Note:The completed project (1c_iv_qrpem.phxproj) is available for reference in …\Examples\NLME.

Set up the Maximum Likelihood Models object

Create a new project called 1c_iv_qrpem.
Import the dataset …\Examples\NLME\Supporting files\model1pkcl.csv.
Click Finish in the File Import Wizard dialog.
Right-click the worksheet and select Send To > Modeling > Maximum Likelihood Models.
Use the option buttons in the Main Mappings panel to map the data types as follows:
AMT to the A1 context
DV to the CObs context
ID and Time are automatically mapped
In the Structure tab, make sure the Parameterization menu is set to Clearance, the Absorption menu to Intravenous, and the Num menu to 1.
Set the Residual Error menu to Multiplicative.
Keep the Stdev value of 0.1.

Note:For PK data with an assumed proportional error model, the use of 0.1 (10% error) as initial input for the standard deviation is often reasonable. Since sigma is also optimized, any prior knowledge is beneficial and can prevent potential confounding between the within (sigma) and between (Omega) subject variability model-based parameters.

Enter initial estimates for the population means

The MCPEM/QRPEM algorithm’s first step requires an initial estimate for the population mean (Fixed Effect) and variance (Random Effect). For each patient, given its data, Phoenix NLME will take these population means and variance (and Sigma) as input and will estimate the most likely set of parameters that explain the patient’s response data. The algorithm finds the sets of values that could explain the same data and, since each set has a different probability in explaining the patient’s data, it defines a distribution (referred to as a posterior distribution).

Select the Parameters > Fixed Effects sub-tab.
Enter the following initial estimates:
tvV = 50
tvCl = 5
Select the Random Effects sub-tab.
Clear the Diag checkbox to specify a full variance covariance matrix.
Enter 1 for all diagonal entries and 0 for off-diagonal.

Starting with initial estimates for the mean and variance and the number of samples to estimate for each patient, the algorithm estimates the individual posterior distributions for each patient. This is used as the sample at the first iteration.

The algorithm then updates the mean and population variances and generates new posterior distributions which are used as the new sample for each patient. The iterations continue, using the same algorithm but with new mean, variances, and sigma.

Usually 50 iterations are enough to reach convergence (i.e., no noticeable change in the means, variances, sigma and log-likelihood). Since the algorithm uses samples, there may be small oscillations in the log-likelihood, but no increasing or decreasing trend once convergence is reached.
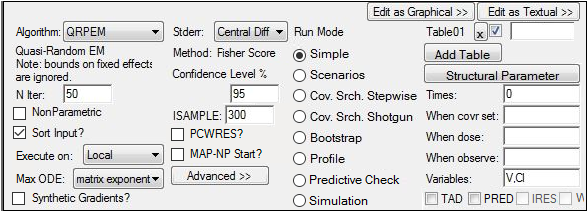
Select the Run Options tab.
In the Algorithm menu, select QRPEM.
Enter 50 iterations for N iter.
To obtain the best model parameters for each patient, add a table.
Click Add Table.
Enter 0 for Times.
Click the Structural Parameter button to list the structural parameters in the Variables field.

Click (Execute icon).
In the Results tab, click Table01 under Output Data.
Table01 reports the individual Cl and V values for each patient (the mode of each individual posterior distribution).
Click Theta under Output Data.

The Theta table shows the final means, variances, and sigma.

Use the MAP

So far in this example, the default method has been used. This method works well when the data are not too rich. The main settings used for the default algorithm include 300 samples for each patient, perform a MAP estimation only at the first iteration, and do a maximum of 50 iterations.

When data are very rich, each patient will be defined most likely by very few Cl and V value sets, with most of the weight on only one set of model parameters. With very rich data, the program can have problems with the default algorithm as the individual posterior variances collapse easily to zero because of there are not enough random samples and because the true posterior variances are very small. When this happens, the estimated posterior variances from iteration two can collapse and it is better to ask the program to do a MAP estimation at each iteration. Increasing the number of samples should also be done.

In the Object Browser, right-click the ML Model object and select Copy.
Right-click the Workflow item and select Paste.
Rename the copied object as MAP.
Select the Run Options tab.
Enter 1000 in the ISAMPLE field.
Click Advanced >>.
Turn on the MAP Assist checkbox.
Execute the object.

For comparison, run the model using the FOCE ELS and FOCE L-B engines instead of QRPEM. QRPEM has a more efficient sampling algorithm, so the number of samples will need to be increased.

This concludes the simple PK population analysis using QRPEM example.