Phoenix provides flexibility in performing weighted nonlinear regression and using weighted regression. Weights are assigned using menu options or by adding weighting values to a dataset. Each operational object in Phoenix that uses weighted values has instructions for using weighting.
There are three ways to assign weights, other than uniform weighting, through the Phoenix user interface:
Weighted least squares: weight by a power of the observed value of Y.
Iterative reweighting: weight by a power of the predicted value of Y.
Reading weights from the dataset: include weight as a column in the dataset.
When using weighted least squares, Phoenix weights each observation by the value of the dependent variable raised to the power of n. That is, WEIGHT=Yn. For example, selecting this option and setting n= –0.5 instructs Phoenix to weight the data by the square root of the reciprocal of observed Y:
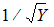
If n has a negative value, and one or more of the Y values are less than or equal to zero, then the corresponding weights are set to zero.
The application scales the weights such that the sum of the weights for each function equals the number of observations with non-zero weights. See “Scaling of weights”.
Iterative Reweighting redefines the weights for each observation to be Fn, where F is the predicted response. For example, selecting this option and setting n= –0.5 instructs Phoenix to weight the data by the square root of reciprocal of the predicted value of Y, i.e.,
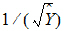
As with Weighted least squares, if N is negative, and one or more of the predicted Y values are less than or equal to zero, then the corresponding weights are set to zero.
Iterative reweighting differs from weighted least squares in that for weighted least squares the weights are fixed. For iteratively re-weighted least squares the parameters change at each iteration, and therefore the predicted values and the weights change at each iteration.
For certain types of models, iterative reweighting can be used to obtain maximum likelihood estimates. For more information see the article by Jennrich and Moore (1975). Maximum likelihood estimation by means of nonlinear least squares. Amer Stat Assoc Proceedings Statistical Computing Section 57–65.
Reading weights from the dataset
It is also possible to have a variable in the dataset that has as its values the weights to use. The weights should be the reciprocal of the variance of the observations. As with Weighted Least Squares, the application scales the weights such that the sum of the weights for each function equals the number of observations with non-zero weights.
When weights are read from a dataset or when weighted least squares is used, the weights for the individual data values are scaled so that the sum of the weights for each function is equal to the number of data values with non-zero weights.
The scaling of the weights has no effect on the model fitting as the weights of the observations are proportionally the same. However, scaling of the weights provides increased numerical stability.
Consider the following example:
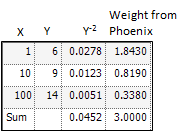
Suppose weighted least squares with the power –2 was specified, which is the same as weighting by 1/Y*Y. The corresponding values are as shown in the third column. Each value of Y–2 is divided by the sum of the values in the third column, and then multiplied by the number of observations, so that:
(0.0277778/.0452254)*3=1.8426238, or 1.843 after rounding.
Note that 0.0278/0.0051 is the same proportion as 1.843/0.338.
