Statistical results and computational formulas

The Descriptive Statistics object creates a Statistics worksheet and a Settings text file in the Results tab. The Statistics worksheet includes summaries of all statistical computations. The Settings file contains user-specified settings.

CI GEO X% Lower: Lower limit of an X% confidence interval for the logs of the data, back-transformed to original scale:

exp(Mean_Log – t_a/2 x SD_Log)

CI GEO X% Upper: Upper limit of an X% confidence interval for the logs of the data, back-transformed to original scale:

exp(Mean_Log + t_a/2 x SD_Log)

where (1 – a)*100 is the percentage given for the confidence interval
and t_a/2 is from the t-distribution with N–1 degrees of freedom.

CI X% Lower: Lower limit of an X% confidence interval for the data (i.e., confidence interval that tells the range that is expected to have X% of the data)

Mean – (t_a/2 x SD)

CI X% Lower GEO Mean: Lower limit of an X% confidence interval for the Geometric Mean:

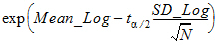
(equivalently, exp of the lower CI for Mean_Log).

CI X% Lower Mean: Lower limit of an X% confidence interval for the mean (i.e., the confidence interval in which the mean exists with X% certainty)

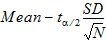
CI X% Lower Var: Lower limit of an X% confidence interval for the variance (i.e., the confidence interval in which the variance exists with X% certainty):

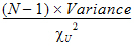
where c_u² is from the c²-distribution with N–1 degrees of freedom.

c_u² cuts off an upper tail of area a/2 where (1–a)*100 is the percentage for the confidence interval.

CI X% Upper: Upper limit of an X% confidence interval for the data:

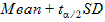
where (1–a)*100 is the percentage given for the confidence interval,
and t_a_/2 is from the t-distribution with N–1 degrees of freedom.

CI X% Upper GEO Mean: Upper limit of an X% confidence interval for the Geometric Mean:

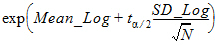
where (1 – a)*100 is the percentage given for the confidence interval,
and t_a_/2 is from the t-distribution with N – 1 degrees of freedom.

CI X% Upper Mean: Upper limit of an X% confidence interval for the mean:

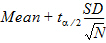
where (1–a)*100 is the percentage given for the confidence interval,
and t_a_/2 is from the t-distribution with N–1 degrees of freedom.

Thus, a 95% confidence level indicates that a=0.05. Note that for N>30, the t-distribution is close to the normal distribution.

CI X% Upper Var: Upper limit of an X% confidence interval for the variance:

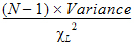
where c_L²is from the c²-distribution with N – 1 degrees of freedom.

c_L² cuts off a lower tail of area a/2 where (1 – a)*100 is the percentage for the confidence interval.

CV%: Coefficient of variation: (SD/Mean)*100

GEO Lower XSD and GEO Upper XSD: Range determined by adding or subtracting “X” log standard deviations from the log-mean, back-transformed to original scale:

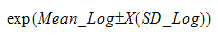
When X=1, this range is equivalent to: (Geometric_Mean/exp(SD_Log) and Geometric_Mean*exp(SD_Log))

Geometric CV%: Geometric coefficient of variation:

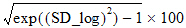
Geometric Mean: N^th root of the product of the N observations. Equivalently, the exponential of the Mean_Log. Each value must be > zero:

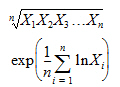
Geometric SD: Geometric standard deviation of the natural logs of the observations exp (SD_Log)

Harmonic Mean: Reciprocal of the arithmetic mean of the reciprocals of the observations:

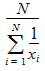
IQR: Interquartile range is the difference between the first and third quartiles (i.e., the middle 50% of the data). IQR is only included in the output when the Include Percentiles checkbox is checked.

KS PValue: Kolmogorov-Smirnov normality test r value. This quantifies the distance between the empirical distribution function of the data and the cumulative distribution function of the Normal distribution. The empirical distribution function F_n for n independent and identically distributed observations X_i is defined as:

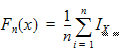
where 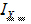is the indicator function and = 1 if 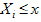, otherwise 0.

The Kolmogorov-Smirnov statistic for a given cumulative distribution function F(x) is:

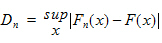
where sup x is the supremum of the set of distances. A r-value is then computed to determine the significance of D_n.

Kurtosis: Sample coefficient of excess (sample excess kurtosis):

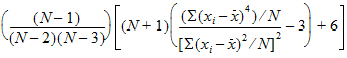
Sample Excess Kurtosis=[Population Excess Kurtosis*(N+1)+6]*(N–1)/[(N–2) x (N–3)]

Kurtosis Pop: Population coefficient of excess (population excess kurtosis):

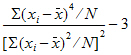
Population Excess Kurtosis=((Sample Excess Kurtosis x (N–2) x (N–3)/(N–1)) –6)/(N+1)

Lower XSD and Upper XSD: Range determined by adding or subtracting X standard deviations from the mean Mean +/– X*SD

Max: Maximum value

Mean: Arithmetic average

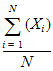
Mean log: Arithmetic average of the natural logs of the observations

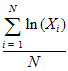
Median: Median value — from the percentiles computations, 50^th percentile.

Min: Minimum value.

N: Number of observations with non-missing data (i.e., numeric observations).

NMiss: Number of observations with missing data (i.e., non-numeric observations such as text or blanks).

NObs: Number of observations (i.e., N+NMiss)

P(ercentiles): The P^th percentile divides the distribution at a point such that P percent of the distribution are below this point. For a sample size of n, the quantile corresponding to the proportion p (0<p<1) is defined as:

Q(p)=(1 – f)*x(j)+f*x(j+1)

where:
     j = int(p*(n+1)), (integer part)
     f = p*(n+1) – j, (fractional part)
     x(j) = the j-th order statistic

The above is used if 1 £ j < n. Otherwise, the empirical quantile is the smallest order statistic for j=0 or the largest order statistic for j=n.

(Definition 6 in Hyndman and Fan, "Sample Quantiles in Statistical Packages", American Statistician, Nov 1996. Equivalent to SAS PCTLDEF 4, Excel PERCENTILE.EXC, and NIST Engineering Statistics Handbook, Section 7.2.6.2, Percentiles.)

Pseudo SD: Jackknife estimate of the standard deviation of the harmonic mean. For n points, x₁, … x_n, the pseudo standard deviation is:

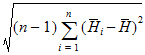
where:

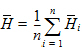
and:

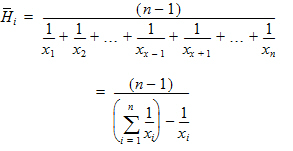
Range: Range of values (maximum value minus minimum value).

SD: Standard Deviation:

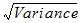
SD Log: Standard deviation of the natural logs of the observations:

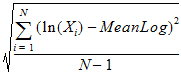
SE: Standard Error:

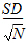
Skewness: Sample coefficient of skewness (sample skewness):

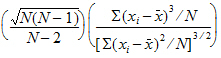
Sample Skewness=Population Skewness*sqrt(N*(N–1))/(N–2)

Skewness Pop: Population coefficient of skewness (population skewness):

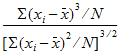
Population Skewness=Sample Skewness*(N–2)/sqrt(N*(N–1))

Sum: Sum of the values in the column mapped to Summary:

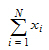
Variance: Unbiased sample variance:

Units

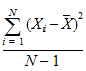
When summary statistics are calculated for a variable with units, some of the output will have units. Assuming that the variable summarized is x and has x-units specified, the units for the summary statistics are:

N, NMiss, NObs: No units
CV%, Geometric CV%: No units
Skewness, Skewness Pop, Kurtosis, Kurtosis Pop, KSP Value: No units
Mean Log, SD Log: No units
Variance: x-unit²
Cl Lower Var, Cl Upper Var: x-unit²
Everything else: x-unit

If more than one Summary variable is mapped, with at least two of those variables having units in the input dataset, and the units differ, a stacked Units column is displayed in the Statistics output worksheet that reports the units of the Summary variables. In cases where the input data does not have units, or the units are all the same, then the units of the statistics are displayed in the column headers.