Sigmoidal and Dissolution models

Model 601 — Hill
Model 602 — Weibull
Model 603 — Double Weibull
Model 604 — Makoid-Banakar
ASCII user model for correlations

Model 601 — Hill

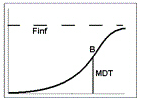y(t) = int + ((Finf – int) * t^b)/(MDT^b + t^b)

where the estimated parameters are:

Finf: amount released at time infinity, using the preferred units for y
MDT: mean dissolution time, in the preferred units for x (time)
b: slope factor (no units)
int: y-intersect; zero (default) or first positive y value in data if estimated, with bounds of zero and 10 times that value

This model includes an optional lag time in the form of a step function, i.e.:

y(t) = int + ((Finf – int) * U(t – t_lag)^b)/(MDT^b + U(t – t_lag)^b)

where U(x) = x if x >= 0; U(x) = 0 if x < 0.

Model 602 — Weibull

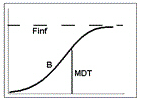y(t) = int + ((Finf – int)(1 – exp[–(t/MDT)^b])

where the estimated parameters are:

Finf: amount released at time infinity, using the preferred units for y
MDT: mean dissolution time, in the preferred units of x (time)
b: slope factor (no units)
int: y-intersect; zero (default) or first positive y value in data if estimated, with bounds of zero and 10 times that value

This model includes an optional lag time in the form of a step function, i.e.:

y(t) = int + ((Finf – int)(1 – exp[–(U(t – t_lag)/MDT)^b])

where U(x) = x if x >= 0; U(x) = 0 if x < 0.

Model 603 — Double Weibull

y(t) = int + f1 * (Finf – int)*(1 – exp[–(t/MDT1)^b1]) +

(1 – f1) * Finf – int (1 – exp[–(t/MDT2)^b2])

where the estimated parameters are:

f1: weighting factor, setting the fraction due to each Weibull (no units)
Finf: amount released at time infinity, using the preferred units for y
MDT1, MDT2: mean dissolution time for each Weibull, (x units)
b1, b2: slope factors (no units)
int: y-intersect; zero (default) or first positive y value in data if estimated, with bounds of zero and 10 times that value

This model includes an optional lag time in the form of a step function, i.e.:

y(t) = int + f1 * (Finf – int) * (1 – exp[–(U(t – t_lag)/MDT1)^b1])
+ (1 – f1) * (Finf - int) * (1 – exp[–(U(t – t_lag)/MDT2)^b2])

where U(x) = x if x >= 0; U(x) = 0 if x < 0.

Model 604 — Makoid-Banakar

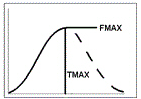y(t) = int + (Fmax - int) * (t/Tmax)^b * exp[b * (1 – t/Tmax)],
for t <= Tmax
y(t)=Fmax, for t > Tmax
where the estimated parameters are:

Fmax: maximum y value, using the preferred units for y
Tmax: time of maximum y value, using the preferred units for x (time)
b: slope factor (no units)
int: y-intersect; zero (default) or first positive y value in data if estimated, with bounds of zero and 10 times that value

This model includes an optional lag time in the form of a step function, i.e.:

y(t) = int + (Fmax - int) * [U(t – t_lag)/Tmax]^b * exp[b * (1 – U(t – t_lag)/Tmax)]

where U(x) = x if x >= 0; U(x) = 0 if x < 0.

Note:The FMAX parameter can be fixed at a certain value by doing one of the following:
– Set the initial estimates option to User-Supplied Initial Parameter Values, and then set initial estimates for any estimated parameters.
– Create a worksheet and use it as an external worksheet for the initial estimates.

ASCII user model for correlations

A custom model for an IVIVC correlation needs to include only the parameter definitions and model equations. No other statements are required.

In the # parameters menu in the Correlation tab, select the number of model parameters.
In the Correlation Estimates panel, enter an initial value for each model parameter.
Edit the statements in the Correlation Code panel to reflect the model. Use the ASCII model syntax and the following keywords that are specific to IVIVC:

•IVINTERP(): This function is used to interpolate dissolution data. A common usage is for X to be the in vivo time, and X is then scaled or shifted by model parameters to yield an in vitro time, which is called T. IVINTERP is then used to interpolate the dissolution data to find the dissolution at time T. The first and last values in the dissolution data are used when T is respectively before or after the time range of the dissolution data.

•DOSEVIVO: This variable contains the dose amount for each formulation. The wizard will translate this variable into the DTA array that is part of the modeling language.

Data deficiencies resulting in missing values for PK parameters

Phoenix reports missing values for PK parameters in the following cases:

Profile with no non-missing observations after dose time, Phoenix reports missing values for all final parameters.

Bolus dosing and <=1 non-missing observation after dose time, Phoenix reports missing values for all final parameters.

Blood/plasma data with no non-zero observation values, Phoenix reports missing values for all final parameters except: Cmax, AUClast, AUCall, AUMClast.

Blood/plasma data with all zero values except one non-zero value at dosing time, Phoenix reports missing values for all final parameters.