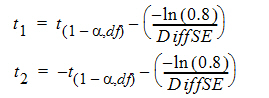See Anderson and Hauck (1983), or page 99 of Chow and Liu (2000). Briefly, the Anderson-Hauck test is based on the hypotheses:
H01: mT – mR < qL vs HA1: mT – mR > qL
H02: mT – mR < qU vs HA2: mT – mR > qU
where qL and qU are the natural logarithm of the Anderson-Hauck limits entered in the bioequivalence options tab. Rejection of both null hypotheses implies bioequivalence. The Anderson-Hauck test statistic is tAH given by:
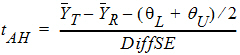
where DiffSE is the standard error of the difference in means. Under the null hypothesis, this test statistic has a noncentral t-distribution.
Power_80_20 in the output is the power to detect a difference in least square means equal to 20% of the reference least squares mean. Percent of Reference to Detect on the Options tab should be the default value of 20%, and the desired result is that Power_80_20 is greater than 0.8 or 80%. (See pg. 142–143 of Chow and Liu (2000).) In general:
PowerOfTest=1 – (probTypeIIError) = probRejectingH0, when H1 is true
Let mT and mR be the true (not observed) values of TestLSM and RefLSM. For this type of power calculation, for the no-transform case, the power is the probability of rejecting: H0(mT = mR) given H1:
|mT – mR| = fractionToDetect(mR)
For ln-transform, and data already ln-transformed, this changes to:
|mT = –mR| = –ln(1– fractionToDetect)
and similarly for log10-transform and data already log10-transformed.
For the default fractionToDetect=0.2, the default a=0.05 (2*a=(100 – Confidence_Level) /100), with no transform on the data and mR > 0:
Power = Pr
(rejecting H0 at the alpha level given the true difference in means = 0.2 x mR)
= 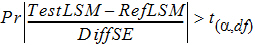
given |mT – mR| = 0.2(mR)
Let:
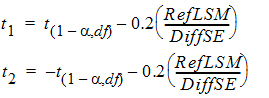
Then:
Power » 1 – [Pr(T > t1) – Pr(T > t2)]
where T has a central t distribution with df=Diff_DF. Note that the second probability may be negligible.
For ln-transform or data already ln-transformed, this changes to: