The Phoenix Model object generates a rather large amount of output:
Phoenix model worksheet output depends on the run mode selected and whether the model is population or individual. The first table indicates what output is created by each run mode and the second table describes the content of each worksheet.
|
Worksheet Output |
Content |
|
BootOmega |
The mean estimated Omega matrix over all sample runs. |
|
BootOmegaStacked |
Estimated Omega matrix for each replication. |
|
BootOmegaStderr |
Estimated standard errors for the Omega matrix over all sample runs. |
|
BootOverall |
Reports the replicate number, the model return code, as well as the likelihood (LL) for all bootstrap runs. |
|
BootSecondary |
Reports secondary parameters over all replicates of a bootstrapped population model. |
|
BootTheta |
Reports fixed effects over all replicates. |
|
BootThetaStacked |
Same information as BootTheta worksheet, but stacked by thetas. |
|
ConvergenceData |
Lists values for each model parameter at each iteration. |
|
Doses |
Reports dosing information for each individual used in the model. |
|
Eta |
Reports post hoc or EBE (empirical Bayesian estimates) of the random effects (eta) for each individual. |
|
EtaCov |
Same information as EtaCovariate and EtaCovariateCat worksheets, but covariates appear as columns so there is one row per subject. |
|
EtaCovariate |
Table by subject of individual continuous covariates and individual post-hoc or EBE of the random effects values. |
|
EtaCovariateCat |
Table by subject of individual categorical covariates and individual post-hoc or EBE of the random effects values. |
|
EtaEta |
Same information as the Eta worksheet, but presented in a different format to facilitate plots. |
|
EtaStacked |
Same as Eta worksheet, but stacked by parameter. |
|
Ind.Quantiles |
Reports the requested quantiles (Column Q) values (Column DV) for the predictive check simulation per ID and IVAR (independent variable) over all the replicates. |
|
InitialEstimates |
Reports the initial estimates used. |
|
NonParEta |
Reports post hoc random effects estimates for each subject when the NonParametric Method is selected. |
|
NonParOverall |
Reports post hoc random effects mean and variance/covariance estimates for the population when the NonParametric Method is selected. |
|
NonParStacked |
Reports marginal and cumulative probabilities of the support point values for each eta, sorted in ascending order and stacked by eta value. |
|
NonParSupport |
Reports a set of support points and their probabilities, which add up to 1, that define the discrete nonparametric distribution obtained by the NonParametric Method. |
|
Observations |
Reports the time elapsed and value for each observation. |
|
Omega |
The estimated Omega matrix, the covariance matrix of the random effects multivariate normal distribution, correlation and summary eta shrinkage statistics. |
|
OmegaStderr |
The estimated standard errors of the Omega estimates. |
|
Overall |
Reports model fit diagnostics. Lists the following columns of information: |
|
•RetCode: Return code indicating the success of the convergence |
|
|
•LogLik: The log likelihood |
|
|
•-2LL: twice the negative log likelihood |
|
|
•AIC: Akaike information Criterion, a goodness of fit measure based on the log likelihood adjusted for the number of parameters (degrees of freedom) in the fit. |
|
|
•BIC: Bayes Information Criterion; similar to AIC but using a different dof adjustment |
|
|
•nParam: Number of parameters (fixed effects parameters+random effects parameters+residual error (eps) parameters) |
|
|
•nObs: Number of observations |
|
|
•nSub: Number of subjects |
|
|
•EpsShrinkage: Epsilon shrinkage, computed as 1-standard deviation (IWRES) for the IWRES values shown on the Residuals worksheet |
|
|
•Condition: An estimate of the degree of collinearity in the linearized design matrix. |
|
|
Note: For covariate searches, this is the only output worksheet generated. To generate the full results, change the Run Mode to Scenarios in the Run Options tab and re-execute. Since the best scenario is selected automatically after the covariate search, it will be used during the Scenarios run. |
|
|
PartialDerivatives |
Reports the partial derivative of each prediction for each fixed effect. |
|
Posthoc |
Reports post hoc values. |
|
|
•stparm(V=tvV*exp(nV)) |
|
|
•stparm(Cl=tvCl*exp(nCl)) |
|
|
Here, tvV and tvCl are fixed effects, and nV and nCl are random effects. |
|
PosthocStacked |
Same as Posthoc worksheet, but stacked by parameter. |
|
PredCheckAll |
Created when Predictive Check mode is used. |
|
PredCheck_TTE |
Created when Predictive Check mode is used and the Time-to-event option is specified on the observation tab. |
|
PredCheck_ObsQ_SimQCI |
Created when Predictive Check mode is used. |
|
PredCheck_SimQ |
Created when Predictive Check mode is used. |
|
Profile |
In Profile runs, summaries of profile runs indicating the parameter, estimate, log-likelihood, return code, delta (perturbation amount) and percent (perturbation percentage) are reported. |
|
Residuals |
Reports model predictions and residuals. (A Resid2 worksheet is also generated if there are two residual errors requested.) |
|
Secondary |
Reports secondary parameters specified by a user, including: |
|
Simulation |
The sort variables, requested IVAR, Simulated DV for the requested Y variables and the name of the Y variables (YVarName) are reported. |
|
Simulation Table 01, Simulation Table 02, ... Population |
Created for simulation TTE when Predictive Check mode is used and the Time-to-event is selected. |
|
StrCovariate |
Table by subject of individual continuous covariates and individual model estimated structural parameter values. |
|
StrCovariateCat |
Table by subject of individual categorical covariates and individual model estimated structural parameter values. |
|
Table01 to Table05 (Optional) |
Optional tables created by the simple run mode or simulation mode for individual models if the user requests them under the Tables Tab. |
|
Theta |
Reports the following: |
|
ThetaCorrelation |
Submatrix of overall parameter correlation matrix corresponding to fixed effect and eps parameters. |
|
ThetaCovariance |
Submatrix of overall parameter covariance matrix corresponding to fixed effect and eps parameters. |
|
VarCovar |
Variance-Covariance matrix of estimates of thetas and omega. |
The success of a Phoenix model fit can usually be diagnosed by the engine return code. The return code is a numeric integer value, usually from 1 to 7, but it can also be zero or negative in special cases when convergence is not requested or achieved. Return codes are presented in the Overall Worksheet(s) in the RetCode column, as well as in the Core Output and Core Status text output.
All Phoenix NLME methods, except QRPEM, are based on the direct numerical optimization of a log likelihood or approximate log likelihood function. The fundamental optimization algorithm used is the well-known unconstrained BFGS quasi-Newton UNCMIN optimizer presented as pseudo-code in Dennis, J.E. and Schnabel, R.B., Numerical Methods for Unconstrained Optimization and Nonlinear Equations, SIAM, 1996 (re-issue of classic 1983 book). Several customized versions of UNCMIN based on this pseudo-code have been implemented in Phoenix for the various engines. The return codes in Phoenix for all engines, except QRPEM, are usually based directly on the ITRMCD return codes of 1 through 5 in UNCMIN. Additional codes of 0, 6, 7, and negative return codes that do not appear in the original UNCMIN have been added to deal with special situations and, in some cases, the meaning of a return code of 4 has been changed. The actual methods of determining the return codes in UNCMIN are rather technical. What follows is a brief summary and the interested user should refer to the reference mentioned above for more detail.
Basically, UNCMIN return codes of 1, 2, and 3 indicate that the optimizer was ‘probably successful’ in reaching at least a local optimum of the log likelihood function, with 1 giving the strongest evidence of success and 3 the weakest. More specifically:
1 means that the ‘scaled gradient’ was reduced below a threshold
2 means that further progress does not seem possible due to relative changes in the parameters becoming too small on successive iterations
3 means that the line search step in the quasi-Newton direction failed to locate a sufficiently better objective value than the current value
4 means that the user-defined maximum number of iterations was reached before any other termination criterion was achieved (note that the meaning of this code has been changed as described below for the FO, Naive pooled, FOCE L-B, and IT2S-EM engines)
5 means that the UNCMIN algorithm failed to compute an acceptable step-size within the allowable internal limit on number of trials.
The FO, Naive pooled, FOCE L-B, and IT2S-EM methods in Phoenix require a sequence of UNCMIN optimizations of a log-likelihood or approximate log-likelihood function. Typically, successful convergence is recognized if the final two members of this sequence give essentially identical results with a UNCMIN return code of 1, 2, or 3. Thus, at least two ‘successful’ UNCMIN optimizations are required for convergence. If convergence is achieved, the return code of 1, 2, or 3 for these engines is the return code from UNCMIN for the final run in the sequence. If these engines do not converge within the user-specified number of UNCMIN attempts (for these engines, the iteration counter is the number of runs of UNCMIN), a return code of 4 is made. If the sequence of UNCMIN optimization is determined to be non-convergent before hitting the maximum number of iterations, a negative return code is made, where the absolute value of the return code is the UNCMIN return code from the final UNCMIN run in the sequence.
Unlike the other UNCMIN-based engines, the FOCE ELS method can sometimes be determined to have converged based on a single UNCMIN run, if the UNCMIN return code is 1 or 2. For a return code of 3, the FOCE ELS algorithm attempts a restart from the final solution so obtained. Here, the iteration counter counts the total number of line searches made throughout all restarts, and thus a return code of 4 means that the total number of such line searches over all attempts has hit the user-specified maximum. If the FOCE ELS algorithm cannot improve upon its original attempt that resulted in a return code of 3, then the results of that attempt are reported with a return code of 3. If, however, better (higher overall log-likelihood) results are obtained, the current attempt then becomes the reference and a new UNCMIN run attempt is made to improve the log-likelihood. The final return code reflects the return code of the best attempt.
To these basic UNCMIN return codes, several others have been added, include 0, 6, 7, and various negative return codes indicating non-convergence. The following table summarizes the meaning of the non-negative integer return codes within the context of each method. Negative return codes generally apply in situations where convergence is not achieved and are also described below.
|
Return Code |
Meaning |
|
0 |
The user ran the engine in evaluation model only, no optimization was requested, and the solution that is returned was the same one entered as a starting solution. |
|
1 |
Convergence was achieved and the final UNCMIN optimization successfully terminated with a scaled gradient below an internal tolerance (this is the ‘best’ possible return code). |
|
2 |
Convergence was achieved and optimization of the final UNCMIN run terminated when parameter change fell below internal tolerance on successive iterations of the final UNCMIN run. |
|
3 |
Convergence was achieved and optimization of the final UNCMIN run terminated when insufficient objective function improvement was made during the line search step along the quasi-Newton direction. QRPEM does not use a return code of 3. |
|
4 |
For FO, FOCE L-B, Naive pooled, and IT2S-EM, the maximum number of UNCMIN runs was reached before any other termination criterion was achieved. |
|
5 |
Optimization was terminated due to internal failure of UNCMIN to find a suitable step size (this is an error termination). |
|
6 |
The user manually terminated the engine from the user interface Stop Early button in the Progress window before convergence. |
|
7 |
If the line search procedure gets into a region where some bad/inappropriate function values are obtained and it fails to find a good one after several attempts, then the engine stops proceeding further and reports the last good results to the user. |
Negative return codes generally indicate some kind of convergence failure and often a more definitive reason for the convergence failure can be found in the Core Status file in the Text Output section of the Results tab or in the file nlme7engine.log (if command line invocation is used). For UNCMIN-based engines, the absolute value of the return code represents the UNCMIN return code on the UNCMIN run that resulted in a determination of convergence failure. QRPEM uses a return code of -4 if non-convergence is detected.
Relatively uncommon, the user can see the return code 40 for FOCE ELS. It indicates that the engine has gone through numerous cycles and was unable to find a solution better than the previous solution by a certain tolerance (.01).
For the Naive Pool engine only, Variance Inflation Factors (VIF) are computed per time entry during simulation runs and presented in several worksheets that tabulate parameter estimates. These are calculated in the same matter as WinNonlin Classical models but are computed regardless of whether the model is simulated or if a fit is run.
VIFs are based on a simple linearization of the model. If the Naive pool engine is run with Number of Iterations > 0, then the linearization is done at the final fitted parameter values. If it is just a simulation, where the model evaluation with Number of iterations=0, then the linearization is done at the initial input values of the parameters. In this case the observed data values never enter into the VIF computation.
For simulations VIFs can be used to compare experimental designs. For fits, if the square roots of the VIFs are multiplied by the epsilon estimate it gives standard error estimates based on the linearized model. Standard error of estimates are normally computed from the Hessian of the objective function. If the Hessian is not successful, the Phoenix Model will then automatically report the standard errors based on successful VIF computation instead. If this occurs, it is indicated in the Core Status text output.
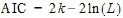 , where:
, where: 